Bayesian Regression Models for Non-Normal Data
Our last post covered how to do bayesian regression for normally distributed data in R using STAN. In this post, we’ll take a look at how to fit a regression model adapted to non-normal model in STAN using two common distributions seen in empirical data, namely, binomial and negative-binomial. As mentioned before in Bayesian modelling we use a set of sampling methods known as Markov Chain Monte Carlo (MCMC), we define a statistical model and find probabilistic estimates for the parameters.
Logistic Regression
The likelihood of a binary outcome, such as pass or fail, is estimated using logistic models (but this model can be extended to include more than two outcomes). This is accomplished by using the logit function to convert a standard regression. The main parameter that we focus on here describes odds of the outcome derived from probabilities and transformed using a logit function. The following is the code for a logistic regression model with one predictor and an intercept.
library(tidyverse)
library(kableExtra)
library(arm)
library(emdbook)
library(rstan)
library(rstanarm)
set.seed(1234)
x1 = rnorm(10000)
z = 1 + 2*x1
pr = 1/(1+exp(-z))
y = rbinom(10000,1,pr)
df = data.frame(y=y,x1=x1)
head(df)%>%kableExtra::kable()
| y | x1 |
|---|---|
| 0 | -1.2070657 |
| 0 | 0.2774292 |
| 1 | 1.0844412 |
| 0 | -2.3456977 |
| 1 | 0.4291247 |
| 1 | 0.5060559 |
glm( y~x1,data=df,family="binomial")%>%summary()%>%pluck(coefficients)%>%kableExtra::kable()
| Estimate | Std. Error | z value | Pr(>|z|) | |
|---|---|---|---|---|
| (Intercept) | 1.036922 | 0.0294863 | 35.16621 | 0 |
| x1 | 1.979352 | 0.0417219 | 47.44162 | 0 |
model_stan = "
data {
int<lower=0> N;
vector[N] x;
int<lower=0,upper=1> y[N];
}
parameters {
real alpha;
real beta;
}
model {
y ~ bernoulli_logit(alpha + beta * x);
}
"
writeLines(model_stan, con = "model_stan.stan")
cat(model_stan)
##
## data {
## int<lower=0> N;
## vector[N] x;
## int<lower=0,upper=1> y[N];
## }
## parameters {
## real alpha;
## real beta;
## }
## model {
## y ~ bernoulli_logit(alpha + beta * x);
## }
##
stan_data <- list(
N = 10000,
x = df$x1,
y = df$y
)
fit_rstan <- rstan::stan(
file = "model_stan.stan",
data = stan_data
)
fit_rstan
## Inference for Stan model: anon_model.
## 4 chains, each with iter=2000; warmup=1000; thin=1;
## post-warmup draws per chain=1000, total post-warmup draws=4000.
##
## mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff
## alpha 1.04 0.00 0.03 0.98 1.02 1.04 1.06 1.10 1936
## beta 1.98 0.00 0.04 1.90 1.95 1.98 2.01 2.06 1804
## lp__ -4339.45 0.03 1.05 -4342.29 -4339.80 -4339.12 -4338.74 -4338.49 1479
## Rhat
## alpha 1
## beta 1
## lp__ 1
##
## Samples were drawn using NUTS(diag_e) at Tue Jun 21 14:03:59 2022.
## For each parameter, n_eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor on split chains (at
## convergence, Rhat=1).
This also can be expanded to several predictors. Below you can find the code as well as some recommendations for making sense of priors.
set.seed(1234)
x1 = rnorm(10000)
x2 = rnorm(10000)
x3 = rnorm(10000)
z = 1 + 2*x1 + 3*x2 - 1*x3
pr = 1/(1+exp(-z))
y = rbinom(10000,1,pr)
df2 = data.frame(y=y,x1=x1,x2=x2,x3=x3)
head(df2)%>%kableExtra::kable()
| y | x1 | x2 | x3 |
|---|---|---|---|
| 0 | -1.2070657 | -1.8168975 | -1.6878627 |
| 1 | 0.2774292 | 0.6271668 | -0.9552011 |
| 1 | 1.0844412 | 0.5180921 | -0.6480572 |
| 0 | -2.3456977 | 0.1409218 | 0.2610342 |
| 1 | 0.4291247 | 1.4572719 | -1.2196940 |
| 1 | 0.5060559 | -0.4935965 | -1.5501888 |
glm( y~x1+x2+x3,data=df2,family="binomial")%>%summary()%>%pluck(coefficients)%>%kableExtra::kable()
| Estimate | Std. Error | z value | Pr(>|z|) | |
|---|---|---|---|---|
| (Intercept) | 1.0108545 | 0.0367817 | 27.48253 | 0 |
| x1 | 1.9471836 | 0.0494298 | 39.39289 | 0 |
| x2 | 2.9598129 | 0.0641890 | 46.11088 | 0 |
| x3 | -0.9448316 | 0.0372918 | -25.33619 | 0 |
model_stan2 ="
data {
int<lower=0> N; // number of observations
int<lower=0> K; // number of predictors
matrix[N, K] X; // predictor matrix
int<lower=0,upper=1> y[N]; // outcome vector
}
parameters {
real alpha; // intercept
vector[K] beta; // coefficients for predictors
}
model {
y ~ bernoulli_logit(alpha + X * beta);
}
"
writeLines(model_stan2, con = "model_stan2.stan")
cat(model_stan2)
##
##
##
## data {
## int<lower=0> N; // number of observations
## int<lower=0> K; // number of predictors
## matrix[N, K] X; // predictor matrix
## int<lower=0,upper=1> y[N]; // outcome vector
## }
## parameters {
## real alpha; // intercept
## vector[K] beta; // coefficients for predictors
## }
## model {
## y ~ bernoulli_logit(alpha + X * beta);
## }
predictors <- df2[,2:4]
stan_data2 <- list(
N = 10000,
K = 3,
X = predictors,
y = df2$y
)
fit_rstan2 <- rstan::stan(
file = "model_stan2.stan",
data = stan_data2
)
## Trying to compile a simple C file
fit_rstan2
## Inference for Stan model: anon_model.
## 4 chains, each with iter=2000; warmup=1000; thin=1;
## post-warmup draws per chain=1000, total post-warmup draws=4000.
##
## mean se_mean sd 2.5% 25% 50% 75% 97.5%
## alpha 1.01 0.00 0.04 0.94 0.99 1.01 1.04 1.08
## beta[1] 1.95 0.00 0.05 1.85 1.92 1.95 1.98 2.05
## beta[2] 2.96 0.00 0.06 2.84 2.92 2.96 3.00 3.09
## beta[3] -0.95 0.00 0.04 -1.02 -0.97 -0.95 -0.92 -0.87
## lp__ -3006.39 0.03 1.38 -3009.82 -3007.07 -3006.08 -3005.37 -3004.68
## n_eff Rhat
## alpha 2845 1
## beta[1] 2338 1
## beta[2] 2221 1
## beta[3] 2160 1
## lp__ 1788 1
##
## Samples were drawn using NUTS(diag_e) at Tue Jun 21 14:05:38 2022.
## For each parameter, n_eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor on split chains (at
## convergence, Rhat=1).
Negative Binomial
The Poisson distribution, which assumes that the variance is equal to the mean, is a popular choice for modelling count data. The data are said to be overdispersed when the variance exceeds the mean, the Negative Binomial distribution can be used in this case. Note that the negative binomial distribution is a probability distribution of discrete random variables.
Let’s say we have a response variable y that has a negative binomial distribution and is influenced by a collection of k explanatory variables X. The negative binomial distribution to model this data has two parameters: The μ or the expected value that need to be positive so a log link function can be used to map the linear predictor (the explanatory variables times the regression parameters) and ϕ which is the overdispersion parameter, where a small value means a large deviation from a Poisson distribution, as ϕ gets larger the negative binomial looks more and more like a Poisson distribution.
Let’s simulate some data and fit a STAN model to them:
N<-100000
df3 <-data.frame(x1=runif(N,-2,2),x2=runif(N,-2,2))
#the model
X<-model.matrix(~x1*x2,df3)
K<-dim(X)[2] #number of regression params
#the regression slopes
betas<-runif(K,-1,1)
#the overdispersion for the simulated data
phi<-5
#simulate the response
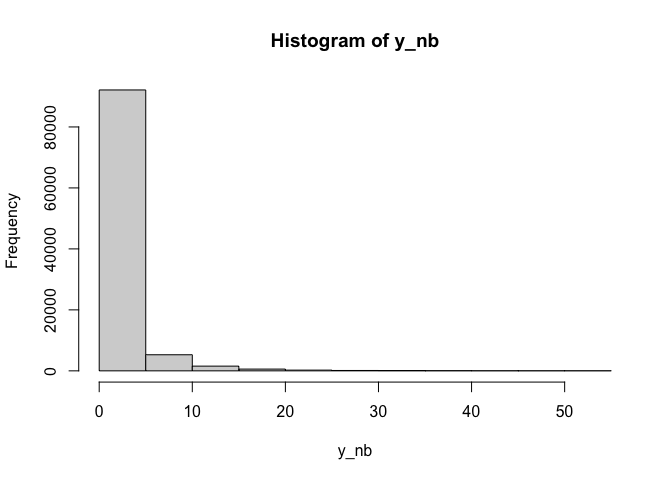
y_nb<-rnbinom(N,size=phi,mu=exp(X%*%betas))
hist(y_nb)
MASS::glm.nb(y_nb ~ X[,2:K])%>%summary()%>%pluck(coefficients)%>%kableExtra::kable()
| Estimate | Std. Error | z value | Pr(>|z|) | |
|---|---|---|---|---|
| (Intercept) | 0.0788902 | 0.0039192 | 20.12938 | 0 |
| X[, 2:K]x1 | -0.0815968 | 0.0032703 | -24.95109 | 0 |
| X[, 2:K]x2 | 0.7941334 | 0.0031740 | 250.20341 | 0 |
| X[, 2:K]x1:x2 | 0.4301282 | 0.0026264 | 163.77308 | 0 |
data {
int N; //the number of observations
int K; //the number of columns in the model matrix
int y[N]; //the response
matrix[N,K] X; //the model matrix
}
parameters {
vector[K] beta; //the regression parameters
real phi; //the overdispersion parameters
}
transformed parameters {
vector[N] mu;//the linear predictor
mu <- exp(X*beta); //using the log link
}
model {
beta[1] ~ cauchy(0,10); //prior for the intercept following Gelman 2008
for(i in 2:K)
beta[i] ~ cauchy(0,2.5);//prior for the slopes following Gelman 2008
y ~ neg_binomial_2(mu,phi);
}
generated quantities {
vector[N] y_rep;
for(n in 1:N){
y_rep[n] <- neg_binomial_2_rng(mu[n],phi); //posterior draws to get posterior predictive checks
}
}
stan_mod = "data {
int N; //the number of observations
int K; //the number of columns in the model matrix
int y[N]; //the response
matrix[N,K] X; //the model matrix
}
parameters {
vector[K] beta; //the regression parameters
real phi; //the overdispersion parameters
}
transformed parameters {
vector[N] mu;//the linear predictor
mu <- exp(X*beta); //using the log link
}
model {
beta[1] ~ cauchy(0,10); //prior for the intercept following Gelman 2008
for(i in 2:K)
beta[i] ~ cauchy(0,2.5);//prior for the slopes following Gelman 2008
y ~ neg_binomial_2(mu,phi);
}
"
writeLines(stan_mod, con = "stan_mod.stan")
cat(stan_mod)
## data {
## int N; //the number of observations
## int K; //the number of columns in the model matrix
## int y[N]; //the response
## matrix[N,K] X; //the model matrix
## }
## parameters {
## vector[K] beta; //the regression parameters
## real phi; //the overdispersion parameters
## }
## transformed parameters {
## vector[N] mu;//the linear predictor
## mu <- exp(X*beta); //using the log link
## }
## model {
## beta[1] ~ cauchy(0,10); //prior for the intercept following Gelman 2008
##
## for(i in 2:K)
## beta[i] ~ cauchy(0,2.5);//prior for the slopes following Gelman 2008
##
## y ~ neg_binomial_2(mu,phi);
## }
stan_data3 <- list(
N = N,
K = K,
X = X,
y = y_nb
)
fit_rstan3 <- rstan::stan(
file = "stan_mod.stan",
data = stan_data3
)
fit_rstan3%>%summary()
## $summary
## mean se_mean sd 2.5% 25%
## beta[1] 7.899069e-02 6.825217e-05 0.0039010484 7.162531e-02 7.635923e-02
## beta[2] -8.157657e-02 5.689044e-05 0.0032236243 -8.786688e-02 -8.376046e-02
## beta[3] 7.941039e-01 5.618629e-05 0.0031476117 7.880475e-01 7.919520e-01
## beta[4] 4.301036e-01 4.552321e-05 0.0026265744 4.248578e-01 4.283603e-01
## phi 4.908958e+00 2.039012e-03 0.0831883094 4.745765e+00 4.854542e+00
Conclusion
This tutorial provided only a quick overview of how to fit logistic and negative binomial regression models with the Bayesian software STAN using the rstan library/API and to extract a collection of useful summaries from the models. Future postings will address the question of outliers and the use of robust linear models.
