Robust t-regression
Motivation
Simple linear regression is a widely used method for estimating the linear relation between two (or more) variables and for predicting the value of one variable (the response variable) based on the value of the other (the explanatory variable). The explanatory variable is typically represented on the x-axis and the response variable on the y-axis for visualising the results of linear regression.
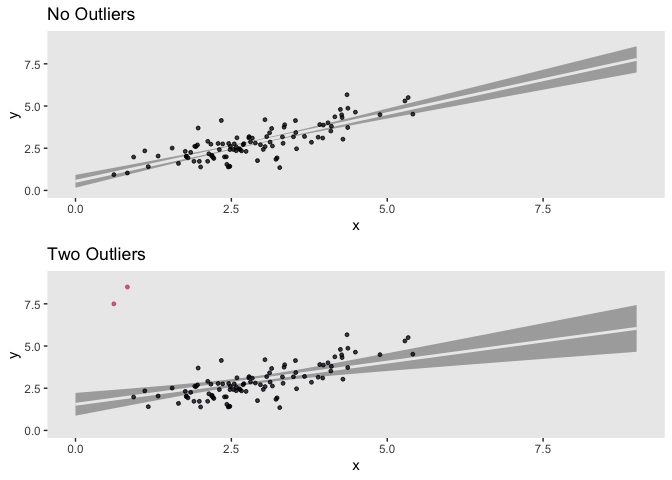
The regression coefficients can be distorted by outlying data points. Due to the normality assumption used by traditional regression techniques, noisy or outlier data can greatly affect their accuracy. Since the normal distribution must move to a new place in the parameter space to best accommodate the outliers in the data, this frequently leads to an underestimate of the relationship between the variables. In a frequentist framework, creating a linear regression model that is resistant to outliers necessitates the use of very complex statistical techniques; however, in a Bayesian framework, we can achieve robustness by simply using the t-distribution. in this context, Robust Regression refers to regression methods which are less sensitive to outliers. Bayesian robust regression uses distributions with wider tails than the normal. This means that outliers will have less of an affect on the models and the regression line would need to move less incorporate those observations since the error distribution will not consider them as unusual.
Utilizing Student’s t density with an unidentified degrees of freedom parameter is a well-liked substitution for normal errors in regression investigations. The Student’s t distribution has heavier tails than the normal for low degrees of freedom, but it leans toward the normal as the degrees of freedom parameter rises. A check on the suitability of the normal is thus made possible by treating the degrees of freedom parameter as an unknown quantity that must be approximated. The degrees of freedom, or parameter ν, of this probability distribution determines how close to normal the distribution is: Low small values of produce a distribution with thicker tails (that is, a greater spread around the mean) than the normal distribution, but big values of (approximately > 30) give a distribution that is quite similar to the normal distribution. As a result, we can allow the distribution of the regression line to be as normal or non-normal as the data imply while still capturing the underlying relationship between the variables by substituting the normal distribution above with a t-distribution and adding as an extra parameter to the model.
Concepts and code
The standard approach to linear regression is defining the equation for a straight line that represents the relationship between the variables as accurately as possible. The equation for the line defines y (the response variable) as a linear function of x (the explanatory variable):
𝑦 = 𝛼 + 𝛽𝑥 + 𝜀
In this equation, ε represents the error in the linear relationship: if no noise were allowed, then the paired x- and y-values would need to be arranged in a perfect straight line (for example, as in y = 2x + 1). Because we assume that the relationship between x and y is truly linear, any variation observed around the regression line must be random noise, and therefore normally distributed. From a probabilistic standpoint, such relationship between the variables could be formalised as
𝑦 ~ 𝓝(𝛼 + 𝛽𝑥, 𝜎)
That is, the response variable follows a normal distribution with mean equal to the regression line, and some standard deviation σ. Such a probability distribution of the regression line is illustrated in the figure below.
The formulation of the robust simple linear regression Bayesian model is given below. We define a t likelihood for the response variable, y, and suitable vague priors on all the model parameters: normal for α and β, half-normal for σ and gamma for ν.
𝑦 ~ 𝓣(𝛼 + 𝛽𝑥, 𝜎, 𝜈)
𝛼, 𝛽 ~ 𝓝(0, 1000)
𝜎 ~ 𝓗𝓝(0, 1000)
𝜈 ~ 𝚪(2, 0.1)
Below you can find R and Stan code for a simple Bayesian t-regression model with nu unknown.
First let’s create data with and without ourliers
library(readr)
library(tidyverse)
library(gridExtra)
library(kableExtra)
library(arm)
library(emdbook)
library(rstan)
library(rstanarm)
library(brms)
s <- matrix(c(1, .8,
.8, 1),
nrow = 2, ncol = 2)
m <- c(3, 3)
set.seed(1234)
data_n <- MASS::mvrnorm(n = 100, mu = m, Sigma = s) %>%
as_tibble() %>%
rename(y = V1, x = V2)
data_n <-
data_n %>%
arrange(x)
head(data_n)%>%kableExtra::kable()
| y | x |
|---|---|
| 0.9335732 | 0.6157783 |
| 1.0317982 | 0.8318674 |
| 1.9763140 | 0.9326985 |
| 2.3439117 | 1.1117327 |
| 1.4059413 | 1.1673553 |
| 2.0360302 | 1.3253002 |
data_o <- data_n
data_o[c(1:2), 1] <- c(7.5, 8.5)
head(data_o)%>%kableExtra::kable()
| y | x |
|---|---|
| 7.500000 | 0.6157783 |
| 8.500000 | 0.8318674 |
| 1.976314 | 0.9326985 |
| 2.343912 | 1.1117327 |
| 1.405941 | 1.1673553 |
| 2.036030 | 1.3253002 |
ols_n <- lm(data = data_n, y ~ 1 + x)
ols_o <- lm(data = data_o, y ~ 1 + x)
p1 <-
ggplot(data = data_n, aes(x = x, y = y)) +
stat_smooth(method = "lm", color = "grey92", fill = "grey67", alpha = 1, fullrange = T) +
geom_point(size = 1, alpha = 3/4) +
scale_x_continuous(limits = c(0, 9)) +
coord_cartesian(xlim = c(0, 9),
ylim = c(0, 9)) +
labs(title = "No Outliers") +
theme(panel.grid = element_blank())
# the data with two outliers
p2 <-
ggplot(data = data_o, aes(x = x, y = y, color = y > 7)) +
stat_smooth(method = "lm", color = "grey92", fill = "grey67", alpha = 1, fullrange = T) +
geom_point(size = 1, alpha = 3/4) +
scale_color_viridis_d(option = "A", end = 4/7) +
scale_x_continuous(limits = c(0, 9)) +
coord_cartesian(xlim = c(0, 9),
ylim = c(0, 9)) +
labs(title = "Two Outliers") +
theme(panel.grid = element_blank(),
legend.position = "none")
grid.arrange(p1 ,p2)
## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'
model_stan = "
data {
int<lower=1> N;
int<lower=0> M;
int<lower=0> P;
vector[N] x;
vector[N] y;
vector[M] x_cred;
vector[P] x_pred;
}
parameters {
real alpha;
real beta;
real<lower=0> sigma;
real<lower=1> nu;
}
transformed parameters {
vector[N] mu = alpha + beta * x;
vector[M] mu_cred = alpha + beta * x_cred;
vector[P] mu_pred = alpha + beta * x_pred;
}
model {
y ~ student_t(nu, mu, sigma);
alpha ~ normal(0, 1000);
beta ~ normal(0, 1000);
sigma ~ normal(0, 1000);
nu ~ gamma(2, 0.1);
}
generated quantities {
real y_pred[P];
for (p in 1:P) {
y_pred[p] = student_t_rng(nu, mu_pred[p], sigma);
}
}
"
writeLines(model_stan, con = "model_stan.stan")
cat(model_stan)
##
## data {
## int<lower=1> N;
## int<lower=0> M;
## int<lower=0> P;
## vector[N] x;
## vector[N] y;
## vector[M] x_cred;
## vector[P] x_pred;
## }
##
## parameters {
## real alpha;
## real beta;
## real<lower=0> sigma;
## real<lower=1> nu;
## }
##
## transformed parameters {
## vector[N] mu = alpha + beta * x;
## vector[M] mu_cred = alpha + beta * x_cred;
## vector[P] mu_pred = alpha + beta * x_pred;
## }
##
## model {
## y ~ student_t(nu, mu, sigma);
## alpha ~ normal(0, 1000);
## beta ~ normal(0, 1000);
## sigma ~ normal(0, 1000);
## nu ~ gamma(2, 0.1);
## }
##
## generated quantities {
## real y_pred[P];
## for (p in 1:P) {
## y_pred[p] = student_t_rng(nu, mu_pred[p], sigma);
## }
## }
##
stan_data <- list(x=data_o$x,
y=data_o$y,
N=length(data_o$y),
M=0, P=0, x_cred=numeric(0), x_pred=numeric(0))
fit_rstan <- rstan::stan(
file = "model_stan.stan",
data = stan_data
)
## Trying to compile a simple C file
## Running /Library/Frameworks/R.framework/Resources/bin/R CMD SHLIB foo.c
## clang -mmacosx-version-min=10.13 -I"/Library/Frameworks/R.framework/Resources/include" -DNDEBUG -I"/Library/Frameworks/R.framework/Versions/4.0/Resources/library/Rcpp/include/" -I"/Library/Frameworks/R.framework/Versions/4.0/Resources/library/RcppEigen/include/" -I"/Library/Frameworks/R.framework/Versions/4.0/Resources/library/RcppEigen/include/unsupported" -I"/Library/Frameworks/R.framework/Versions/4.0/Resources/library/BH/include" -I"/Library/Frameworks/R.framework/Versions/4.0/Resources/library/StanHeaders/include/src/" -I"/Library/Frameworks/R.framework/Versions/4.0/Resources/library/StanHeaders/include/" -I"/Library/Frameworks/R.framework/Versions/4.0/Resources/library/RcppParallel/include/" -I"/Library/Frameworks/R.framework/Versions/4.0/Resources/library/rstan/include" -DEIGEN_NO_DEBUG -DBOOST_DISABLE_ASSERTS -DBOOST_PENDING_INTEGER_LOG2_HPP -DSTAN_THREADS -DUSE_STANC3 -DSTRICT_R_HEADERS -DBOOST_PHOENIX_NO_VARIADIC_EXPRESSION -DBOOST_NO_AUTO_PTR -include '/Library/Frameworks/R.framework/Versions/4.0/Resources/library/StanHeaders/include/stan/math/prim/fun/Eigen.hpp' -D_REENTRANT -DRCPP_PARALLEL_USE_TBB=1 -I/usr/local/include -fPIC -Wall -g -O2 -c foo.c -o foo.o
## In file included from <built-in>:1:
## In file included from /Library/Frameworks/R.framework/Versions/4.0/Resources/library/StanHeaders/include/stan/math/prim/fun/Eigen.hpp:22:
## In file included from /Library/Frameworks/R.framework/Versions/4.0/Resources/library/RcppEigen/include/Eigen/Dense:1:
## In file included from /Library/Frameworks/R.framework/Versions/4.0/Resources/library/RcppEigen/include/Eigen/Core:88:
## /Library/Frameworks/R.framework/Versions/4.0/Resources/library/RcppEigen/include/Eigen/src/Core/util/Macros.h:628:1: error: unknown type name 'namespace'
## namespace Eigen {
## ^
## /Library/Frameworks/R.framework/Versions/4.0/Resources/library/RcppEigen/include/Eigen/src/Core/util/Macros.h:628:16: error: expected ';' after top level declarator
## namespace Eigen {
## ^
## ;
## In file included from <built-in>:1:
## In file included from /Library/Frameworks/R.framework/Versions/4.0/Resources/library/StanHeaders/include/stan/math/prim/fun/Eigen.hpp:22:
## In file included from /Library/Frameworks/R.framework/Versions/4.0/Resources/library/RcppEigen/include/Eigen/Dense:1:
## /Library/Frameworks/R.framework/Versions/4.0/Resources/library/RcppEigen/include/Eigen/Core:96:10: fatal error: 'complex' file not found
## #include <complex>
## ^~~~~~~~~
## 3 errors generated.
## make: *** [foo.o] Error 1
##
## SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 1).
## Chain 1:
## Chain 1: Gradient evaluation took 3.9e-05 seconds
## Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.39 seconds.
## Chain 1: Adjust your expectations accordingly!
## Chain 1:
## Chain 1:
## Chain 1: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 1: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 1: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 1: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 1: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 1: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 1: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 1: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 1: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 1: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 1: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 1: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 1:
## Chain 1: Elapsed Time: 0.114 seconds (Warm-up)
## Chain 1: 0.122 seconds (Sampling)
## Chain 1: 0.236 seconds (Total)
## Chain 1:
##
## SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 2).
## Chain 2:
## Chain 2: Gradient evaluation took 1.3e-05 seconds
## Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.13 seconds.
## Chain 2: Adjust your expectations accordingly!
## Chain 2:
## Chain 2:
## Chain 2: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 2: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 2: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 2: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 2: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 2: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 2: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 2: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 2: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 2: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 2: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 2: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 2:
## Chain 2: Elapsed Time: 0.126 seconds (Warm-up)
## Chain 2: 0.11 seconds (Sampling)
## Chain 2: 0.236 seconds (Total)
## Chain 2:
##
## SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 3).
## Chain 3:
## Chain 3: Gradient evaluation took 9e-06 seconds
## Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.09 seconds.
## Chain 3: Adjust your expectations accordingly!
## Chain 3:
## Chain 3:
## Chain 3: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 3: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 3: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 3: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 3: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 3: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 3: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 3: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 3: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 3: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 3: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 3: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 3:
## Chain 3: Elapsed Time: 0.122 seconds (Warm-up)
## Chain 3: 0.111 seconds (Sampling)
## Chain 3: 0.233 seconds (Total)
## Chain 3:
##
## SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 4).
## Chain 4:
## Chain 4: Gradient evaluation took 1.1e-05 seconds
## Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.11 seconds.
## Chain 4: Adjust your expectations accordingly!
## Chain 4:
## Chain 4:
## Chain 4: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 4: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 4: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 4: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 4: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 4: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 4: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 4: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 4: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 4: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 4: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 4: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 4:
## Chain 4: Elapsed Time: 0.134 seconds (Warm-up)
## Chain 4: 0.113 seconds (Sampling)
## Chain 4: 0.247 seconds (Total)
## Chain 4:
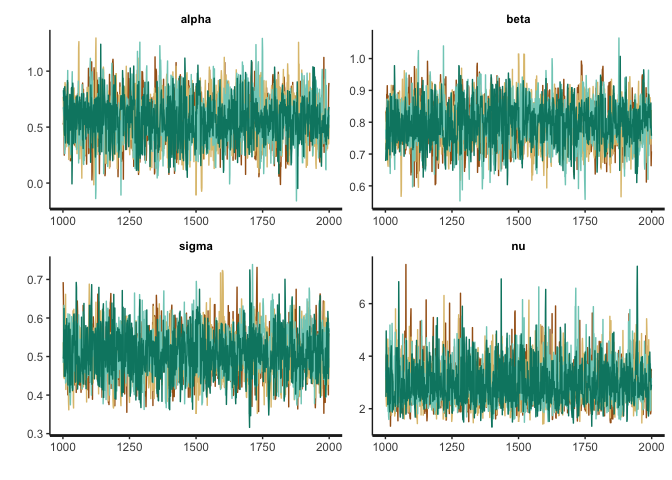
trace <- stan_trace(fit_rstan, pars=c("alpha", "beta", "sigma", "nu"))
trace + scale_color_brewer(type = "div") + theme(legend.position = "none")
## Scale for 'colour' is already present. Adding another scale for 'colour',
## which will replace the existing scale.
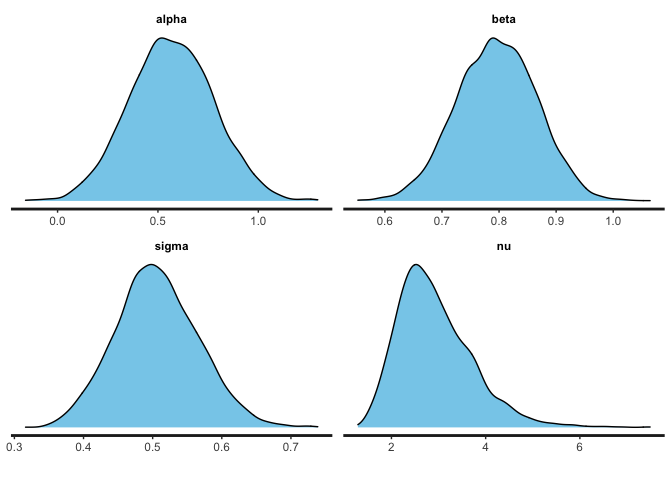
stan_dens(fit_rstan, pars=c("alpha", "beta", "sigma", "nu"), fill = "skyblue")
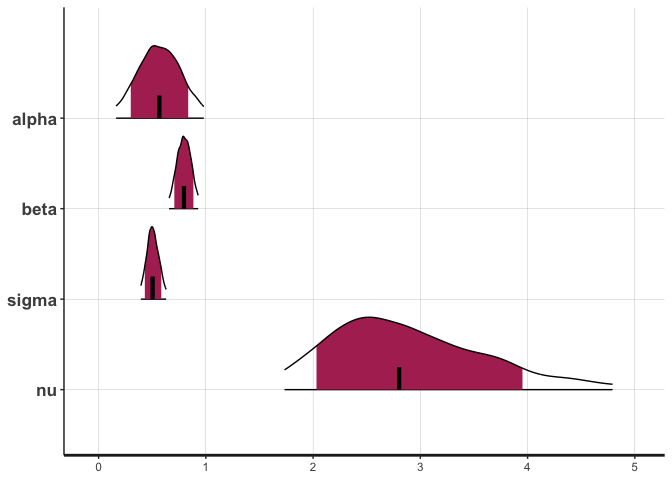
stan_plot(fit_rstan, pars=c("alpha", "beta", "sigma", "nu"), show_density = TRUE, fill_color = "maroon")
## ci_level: 0.8 (80% intervals)
## outer_level: 0.95 (95% intervals)
Bayesian regression models can be used to estimate highest posterior density or credible intervals (intervals of the distribution of the regression linefor), and prediction values, through predictive posterior distributions. More specifically, the prediction intervals are obtained by first drawing samples of the mean response at specific x-values of interest and then, for each of these samples, randomly selecting a y-value from a t-distribution with location mu pred. In contrast, the credible intervals are obtained by drawing MCMC samples of the mean response at regularly spaced points along the x-axis. The distributions of mu cred and y pred are represented, respectively, by the credible and prediction intervals.
x.cred = seq(from=min(data_o$x),
to=max(data_o$x),
length.out=50)
x.pred = c(0, 8)
stan_data2 <- list(x=data_o$x,
y=data_o$y,
N=length(data_o$y),
x_cred=x.cred,
x_pred=x.pred,
M=length(x.cred),
P=length(x.pred))
fit_rstan2 <- rstan::stan(
file = "model_stan.stan",
data = stan_data2
)
##
## SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 1).
## Chain 1:
## Chain 1: Gradient evaluation took 2.6e-05 seconds
## Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.26 seconds.
## Chain 1: Adjust your expectations accordingly!
## Chain 1:
## Chain 1:
## Chain 1: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 1: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 1: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 1: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 1: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 1: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 1: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 1: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 1: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 1: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 1: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 1: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 1:
## Chain 1: Elapsed Time: 0.157 seconds (Warm-up)
## Chain 1: 0.134 seconds (Sampling)
## Chain 1: 0.291 seconds (Total)
## Chain 1:
##
## SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 2).
## Chain 2:
## Chain 2: Gradient evaluation took 1e-05 seconds
## Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.1 seconds.
## Chain 2: Adjust your expectations accordingly!
## Chain 2:
## Chain 2:
## Chain 2: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 2: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 2: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 2: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 2: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 2: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 2: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 2: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 2: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 2: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 2: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 2: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 2:
## Chain 2: Elapsed Time: 0.148 seconds (Warm-up)
## Chain 2: 0.101 seconds (Sampling)
## Chain 2: 0.249 seconds (Total)
## Chain 2:
##
## SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 3).
## Chain 3:
## Chain 3: Gradient evaluation took 1.4e-05 seconds
## Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.14 seconds.
## Chain 3: Adjust your expectations accordingly!
## Chain 3:
## Chain 3:
## Chain 3: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 3: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 3: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 3: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 3: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 3: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 3: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 3: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 3: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 3: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 3: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 3: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 3:
## Chain 3: Elapsed Time: 0.165 seconds (Warm-up)
## Chain 3: 0.132 seconds (Sampling)
## Chain 3: 0.297 seconds (Total)
## Chain 3:
##
## SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 4).
## Chain 4:
## Chain 4: Gradient evaluation took 1.2e-05 seconds
## Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.12 seconds.
## Chain 4: Adjust your expectations accordingly!
## Chain 4:
## Chain 4:
## Chain 4: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 4: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 4: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 4: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 4: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 4: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 4: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 4: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 4: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 4: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 4: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 4: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 4:
## Chain 4: Elapsed Time: 0.151 seconds (Warm-up)
## Chain 4: 0.145 seconds (Sampling)
## Chain 4: 0.296 seconds (Total)
## Chain 4:
For each value in x.cred, the mu cred parameter’s MCMC samples are contained in a separate column of mu.cred. In a similar manner, the columns of y.pred include the MCMC samples of the posterior expected response values (y pred values) for the x-values in x.pred.
summary(extract(fit_rstan2, "mu_cred")[[1]])%>%kableExtra::kable()
| V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | V10 | V11 | V12 | V13 | V14 | V15 | V16 | V17 | V18 | V19 | V20 | V21 | V22 | V23 | V24 | V25 | V26 | V27 | V28 | V29 | V30 | V31 | V32 | V33 | V34 | V35 | V36 | V37 | V38 | V39 | V40 | V41 | V42 | V43 | V44 | V45 | V46 | V47 | V48 | V49 | V50 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min. :0.4535 | Min. :0.553 | Min. :0.6525 | Min. :0.752 | Min. :0.8515 | Min. :0.951 | Min. :1.051 | Min. :1.150 | Min. :1.250 | Min. :1.349 | Min. :1.449 | Min. :1.548 | Min. :1.642 | Min. :1.734 | Min. :1.826 | Min. :1.918 | Min. :2.010 | Min. :2.102 | Min. :2.194 | Min. :2.285 | Min. :2.377 | Min. :2.458 | Min. :2.531 | Min. :2.603 | Min. :2.675 | Min. :2.747 | Min. :2.820 | Min. :2.892 | Min. :2.964 | Min. :3.037 | Min. :3.109 | Min. :3.181 | Min. :3.245 | Min. :3.297 | Min. :3.349 | Min. :3.401 | Min. :3.453 | Min. :3.505 | Min. :3.557 | Min. :3.609 | Min. :3.661 | Min. :3.713 | Min. :3.765 | Min. :3.817 | Min. :3.869 | Min. :3.921 | Min. :3.973 | Min. :4.025 | Min. :4.077 | Min. :4.129 | |
| 1st Qu.:0.9464 | 1st Qu.:1.029 | 1st Qu.:1.1113 | 1st Qu.:1.193 | 1st Qu.:1.2762 | 1st Qu.:1.359 | 1st Qu.:1.441 | 1st Qu.:1.524 | 1st Qu.:1.605 | 1st Qu.:1.688 | 1st Qu.:1.769 | 1st Qu.:1.851 | 1st Qu.:1.931 | 1st Qu.:2.012 | 1st Qu.:2.093 | 1st Qu.:2.174 | 1st Qu.:2.254 | 1st Qu.:2.335 | 1st Qu.:2.415 | 1st Qu.:2.495 | 1st Qu.:2.574 | 1st Qu.:2.654 | 1st Qu.:2.733 | 1st Qu.:2.810 | 1st Qu.:2.888 | 1st Qu.:2.966 | 1st Qu.:3.043 | 1st Qu.:3.119 | 1st Qu.:3.195 | 1st Qu.:3.270 | 1st Qu.:3.344 | 1st Qu.:3.419 | 1st Qu.:3.493 | 1st Qu.:3.569 | 1st Qu.:3.644 | 1st Qu.:3.717 | 1st Qu.:3.792 | 1st Qu.:3.867 | 1st Qu.:3.942 | 1st Qu.:4.015 | 1st Qu.:4.089 | 1st Qu.:4.163 | 1st Qu.:4.237 | 1st Qu.:4.311 | 1st Qu.:4.386 | 1st Qu.:4.460 | 1st Qu.:4.534 | 1st Qu.:4.608 | 1st Qu.:4.681 | 1st Qu.:4.753 | |
| Median :1.0605 | Median :1.138 | Median :1.2165 | Median :1.295 | Median :1.3724 | Median :1.450 | Median :1.528 | Median :1.606 | Median :1.684 | Median :1.762 | Median :1.840 | Median :1.918 | Median :1.996 | Median :2.074 | Median :2.152 | Median :2.230 | Median :2.308 | Median :2.386 | Median :2.463 | Median :2.542 | Median :2.619 | Median :2.698 | Median :2.775 | Median :2.853 | Median :2.931 | Median :3.010 | Median :3.087 | Median :3.165 | Median :3.243 | Median :3.322 | Median :3.400 | Median :3.478 | Median :3.557 | Median :3.634 | Median :3.713 | Median :3.790 | Median :3.868 | Median :3.947 | Median :4.024 | Median :4.102 | Median :4.180 | Median :4.257 | Median :4.335 | Median :4.413 | Median :4.491 | Median :4.569 | Median :4.647 | Median :4.726 | Median :4.803 | Median :4.881 | |
| Mean :1.0605 | Mean :1.138 | Mean :1.2164 | Mean :1.294 | Mean :1.3723 | Mean :1.450 | Mean :1.528 | Mean :1.606 | Mean :1.684 | Mean :1.762 | Mean :1.840 | Mean :1.918 | Mean :1.996 | Mean :2.074 | Mean :2.152 | Mean :2.230 | Mean :2.308 | Mean :2.386 | Mean :2.464 | Mean :2.542 | Mean :2.619 | Mean :2.697 | Mean :2.775 | Mean :2.853 | Mean :2.931 | Mean :3.009 | Mean :3.087 | Mean :3.165 | Mean :3.243 | Mean :3.321 | Mean :3.399 | Mean :3.477 | Mean :3.555 | Mean :3.633 | Mean :3.711 | Mean :3.789 | Mean :3.867 | Mean :3.945 | Mean :4.023 | Mean :4.101 | Mean :4.178 | Mean :4.256 | Mean :4.334 | Mean :4.412 | Mean :4.490 | Mean :4.568 | Mean :4.646 | Mean :4.724 | Mean :4.802 | Mean :4.880 | |
| 3rd Qu.:1.1739 | 3rd Qu.:1.247 | 3rd Qu.:1.3213 | 3rd Qu.:1.394 | 3rd Qu.:1.4688 | 3rd Qu.:1.543 | 3rd Qu.:1.616 | 3rd Qu.:1.691 | 3rd Qu.:1.766 | 3rd Qu.:1.840 | 3rd Qu.:1.915 | 3rd Qu.:1.989 | 3rd Qu.:2.063 | 3rd Qu.:2.137 | 3rd Qu.:2.212 | 3rd Qu.:2.286 | 3rd Qu.:2.362 | 3rd Qu.:2.436 | 3rd Qu.:2.512 | 3rd Qu.:2.587 | 3rd Qu.:2.663 | 3rd Qu.:2.740 | 3rd Qu.:2.817 | 3rd Qu.:2.895 | 3rd Qu.:2.973 | 3rd Qu.:3.052 | 3rd Qu.:3.132 | 3rd Qu.:3.212 | 3rd Qu.:3.292 | 3rd Qu.:3.372 | 3rd Qu.:3.453 | 3rd Qu.:3.535 | 3rd Qu.:3.616 | 3rd Qu.:3.698 | 3rd Qu.:3.779 | 3rd Qu.:3.861 | 3rd Qu.:3.943 | 3rd Qu.:4.025 | 3rd Qu.:4.107 | 3rd Qu.:4.189 | 3rd Qu.:4.271 | 3rd Qu.:4.353 | 3rd Qu.:4.436 | 3rd Qu.:4.518 | 3rd Qu.:4.600 | 3rd Qu.:4.682 | 3rd Qu.:4.765 | 3rd Qu.:4.847 | 3rd Qu.:4.929 | 3rd Qu.:5.012 | |
| Max. :1.6368 | Max. :1.697 | Max. :1.7566 | Max. :1.817 | Max. :1.8764 | Max. :1.936 | Max. :1.996 | Max. :2.056 | Max. :2.116 | Max. :2.176 | Max. :2.236 | Max. :2.296 | Max. :2.356 | Max. :2.416 | Max. :2.475 | Max. :2.535 | Max. :2.595 | Max. :2.655 | Max. :2.729 | Max. :2.811 | Max. :2.893 | Max. :2.974 | Max. :3.056 | Max. :3.138 | Max. :3.220 | Max. :3.301 | Max. :3.383 | Max. :3.465 | Max. :3.547 | Max. :3.628 | Max. :3.710 | Max. :3.792 | Max. :3.874 | Max. :3.955 | Max. :4.037 | Max. :4.123 | Max. :4.222 | Max. :4.321 | Max. :4.420 | Max. :4.520 | Max. :4.619 | Max. :4.718 | Max. :4.818 | Max. :4.917 | Max. :5.016 | Max. :5.116 | Max. :5.215 | Max. :5.314 | Max. :5.414 | Max. :5.513 |
summary(extract(fit_rstan2, "y_pred")[[1]])%>%kableExtra::kable()
| V1 | V2 | |
|---|---|---|
| Min. :-36.0432 | Min. :-7.818 | |
| 1st Qu.: 0.1482 | 1st Qu.: 6.466 | |
| Median : 0.5704 | Median : 6.954 | |
| Mean : 0.5951 | Mean : 6.946 | |
| 3rd Qu.: 1.0130 | 3rd Qu.: 7.431 | |
| Max. : 19.3150 | Max. :23.107 |
These models can be also etimated through brms package’s API for Stan as follows
M_gaussian <-
brm(data = data_o,
family = gaussian,
y ~ 1 + x,
prior = c(prior(normal(0, 10), class = Intercept),
prior(normal(0, 10), class = b),
prior(cauchy(0, 1), class = sigma)),
seed = 1)
##
## SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 1).
## Chain 1:
## Chain 1: Gradient evaluation took 2.3e-05 seconds
## Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.23 seconds.
## Chain 1: Adjust your expectations accordingly!
## Chain 1:
## Chain 1:
## Chain 1: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 1: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 1: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 1: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 1: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 1: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 1: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 1: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 1: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 1: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 1: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 1: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 1:
## Chain 1: Elapsed Time: 0.02 seconds (Warm-up)
## Chain 1: 0.019 seconds (Sampling)
## Chain 1: 0.039 seconds (Total)
## Chain 1:
##
## SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 2).
## Chain 2:
## Chain 2: Gradient evaluation took 5e-06 seconds
## Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds.
## Chain 2: Adjust your expectations accordingly!
## Chain 2:
## Chain 2:
## Chain 2: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 2: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 2: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 2: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 2: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 2: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 2: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 2: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 2: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 2: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 2: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 2: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 2:
## Chain 2: Elapsed Time: 0.019 seconds (Warm-up)
## Chain 2: 0.016 seconds (Sampling)
## Chain 2: 0.035 seconds (Total)
## Chain 2:
##
## SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 3).
## Chain 3:
## Chain 3: Gradient evaluation took 5e-06 seconds
## Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds.
## Chain 3: Adjust your expectations accordingly!
## Chain 3:
## Chain 3:
## Chain 3: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 3: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 3: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 3: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 3: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 3: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 3: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 3: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 3: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 3: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 3: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 3: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 3:
## Chain 3: Elapsed Time: 0.019 seconds (Warm-up)
## Chain 3: 0.016 seconds (Sampling)
## Chain 3: 0.035 seconds (Total)
## Chain 3:
##
## SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 4).
## Chain 4:
## Chain 4: Gradient evaluation took 4e-06 seconds
## Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.04 seconds.
## Chain 4: Adjust your expectations accordingly!
## Chain 4:
## Chain 4:
## Chain 4: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 4: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 4: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 4: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 4: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 4: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 4: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 4: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 4: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 4: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 4: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 4: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 4:
## Chain 4: Elapsed Time: 0.019 seconds (Warm-up)
## Chain 4: 0.018 seconds (Sampling)
## Chain 4: 0.037 seconds (Total)
## Chain 4:
summary(M_gaussian)
## Family: gaussian
## Links: mu = identity; sigma = identity
## Formula: y ~ 1 + x
## Data: data_o (Number of observations: 100)
## Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
## total post-warmup draws = 4000
##
## Population-Level Effects:
## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## Intercept 1.56 0.34 0.88 2.22 1.00 3889 2871
## x 0.50 0.11 0.28 0.72 1.00 3941 2995
##
## Family Specific Parameters:
## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## sigma 1.13 0.08 0.98 1.30 1.00 3719 2831
##
## Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
## and Tail_ESS are effective sample size measures, and Rhat is the potential
## scale reduction factor on split chains (at convergence, Rhat = 1).
M_student <-
brm(data = data_o, family = student,
y ~ 1 + x,
prior = c(prior(normal(0, 10), class = Intercept),
prior(normal(0, 10), class = b),
prior(gamma(4, 1), class = nu),
prior(cauchy(0, 1), class = sigma)),
seed = 1)
## Compiling Stan program...
## Trying to compile a simple C file
## Running /Library/Frameworks/R.framework/Resources/bin/R CMD SHLIB foo.c
## clang -mmacosx-version-min=10.13 -I"/Library/Frameworks/R.framework/Resources/include" -DNDEBUG -I"/Library/Frameworks/R.framework/Versions/4.0/Resources/library/Rcpp/include/" -I"/Library/Frameworks/R.framework/Versions/4.0/Resources/library/RcppEigen/include/" -I"/Library/Frameworks/R.framework/Versions/4.0/Resources/library/RcppEigen/include/unsupported" -I"/Library/Frameworks/R.framework/Versions/4.0/Resources/library/BH/include" -I"/Library/Frameworks/R.framework/Versions/4.0/Resources/library/StanHeaders/include/src/" -I"/Library/Frameworks/R.framework/Versions/4.0/Resources/library/StanHeaders/include/" -I"/Library/Frameworks/R.framework/Versions/4.0/Resources/library/RcppParallel/include/" -I"/Library/Frameworks/R.framework/Versions/4.0/Resources/library/rstan/include" -DEIGEN_NO_DEBUG -DBOOST_DISABLE_ASSERTS -DBOOST_PENDING_INTEGER_LOG2_HPP -DSTAN_THREADS -DUSE_STANC3 -DSTRICT_R_HEADERS -DBOOST_PHOENIX_NO_VARIADIC_EXPRESSION -DBOOST_NO_AUTO_PTR -include '/Library/Frameworks/R.framework/Versions/4.0/Resources/library/StanHeaders/include/stan/math/prim/fun/Eigen.hpp' -D_REENTRANT -DRCPP_PARALLEL_USE_TBB=1 -I/usr/local/include -fPIC -Wall -g -O2 -c foo.c -o foo.o
## In file included from <built-in>:1:
## In file included from /Library/Frameworks/R.framework/Versions/4.0/Resources/library/StanHeaders/include/stan/math/prim/fun/Eigen.hpp:22:
## In file included from /Library/Frameworks/R.framework/Versions/4.0/Resources/library/RcppEigen/include/Eigen/Dense:1:
## In file included from /Library/Frameworks/R.framework/Versions/4.0/Resources/library/RcppEigen/include/Eigen/Core:88:
## /Library/Frameworks/R.framework/Versions/4.0/Resources/library/RcppEigen/include/Eigen/src/Core/util/Macros.h:628:1: error: unknown type name 'namespace'
## namespace Eigen {
## ^
## /Library/Frameworks/R.framework/Versions/4.0/Resources/library/RcppEigen/include/Eigen/src/Core/util/Macros.h:628:16: error: expected ';' after top level declarator
## namespace Eigen {
## ^
## ;
## In file included from <built-in>:1:
## In file included from /Library/Frameworks/R.framework/Versions/4.0/Resources/library/StanHeaders/include/stan/math/prim/fun/Eigen.hpp:22:
## In file included from /Library/Frameworks/R.framework/Versions/4.0/Resources/library/RcppEigen/include/Eigen/Dense:1:
## /Library/Frameworks/R.framework/Versions/4.0/Resources/library/RcppEigen/include/Eigen/Core:96:10: fatal error: 'complex' file not found
## #include <complex>
## ^~~~~~~~~
## 3 errors generated.
## make: *** [foo.o] Error 1
## Start sampling
##
## SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 1).
## Chain 1:
## Chain 1: Gradient evaluation took 0.000456 seconds
## Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 4.56 seconds.
## Chain 1: Adjust your expectations accordingly!
## Chain 1:
## Chain 1:
## Chain 1: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 1: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 1: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 1: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 1: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 1: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 1: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 1: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 1: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 1: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 1: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 1: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 1:
## Chain 1: Elapsed Time: 0.07 seconds (Warm-up)
## Chain 1: 0.063 seconds (Sampling)
## Chain 1: 0.133 seconds (Total)
## Chain 1:
##
## SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 2).
## Chain 2:
## Chain 2: Gradient evaluation took 1.8e-05 seconds
## Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.18 seconds.
## Chain 2: Adjust your expectations accordingly!
## Chain 2:
## Chain 2:
## Chain 2: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 2: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 2: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 2: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 2: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 2: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 2: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 2: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 2: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 2: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 2: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 2: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 2:
## Chain 2: Elapsed Time: 0.069 seconds (Warm-up)
## Chain 2: 0.066 seconds (Sampling)
## Chain 2: 0.135 seconds (Total)
## Chain 2:
##
## SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 3).
## Chain 3:
## Chain 3: Gradient evaluation took 1.3e-05 seconds
## Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.13 seconds.
## Chain 3: Adjust your expectations accordingly!
## Chain 3:
## Chain 3:
## Chain 3: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 3: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 3: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 3: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 3: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 3: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 3: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 3: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 3: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 3: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 3: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 3: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 3:
## Chain 3: Elapsed Time: 0.071 seconds (Warm-up)
## Chain 3: 0.063 seconds (Sampling)
## Chain 3: 0.134 seconds (Total)
## Chain 3:
##
## SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 4).
## Chain 4:
## Chain 4: Gradient evaluation took 2.5e-05 seconds
## Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.25 seconds.
## Chain 4: Adjust your expectations accordingly!
## Chain 4:
## Chain 4:
## Chain 4: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 4: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 4: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 4: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 4: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 4: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 4: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 4: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 4: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 4: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 4: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 4: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 4:
## Chain 4: Elapsed Time: 0.07 seconds (Warm-up)
## Chain 4: 0.065 seconds (Sampling)
## Chain 4: 0.135 seconds (Total)
## Chain 4:
summary(M_student)
## Family: student
## Links: mu = identity; sigma = identity; nu = identity
## Formula: y ~ 1 + x
## Data: data_o (Number of observations: 100)
## Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
## total post-warmup draws = 4000
##
## Population-Level Effects:
## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## Intercept 0.56 0.20 0.17 0.96 1.00 3835 2836
## x 0.80 0.07 0.66 0.93 1.00 3836 3084
##
## Family Specific Parameters:
## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## sigma 0.50 0.06 0.39 0.62 1.00 3183 2799
## nu 2.80 0.70 1.71 4.49 1.00 3564 2917
##
## Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
## and Tail_ESS are effective sample size measures, and Rhat is the potential
## scale reduction factor on split chains (at convergence, Rhat = 1).
Conclusion
In this post, we have provided a simple Bayesian approach to robustly estimate both parameters β and σ of a simple linear regression where the estiamtes are robust to the variance of the error term. The specificity of this approach is to replace the traditional normal assumption on the dependant variable by a heavy-tailed t-distribution assumption. Robusness against outliers comes at a price of a loss of efficiency, especially when the observations are normally distributed. This is a low premium that comes with the robust alternatives that offers a large protection against over-fiting.
