Partially Observable Markov Decision Process (POMDP) in R
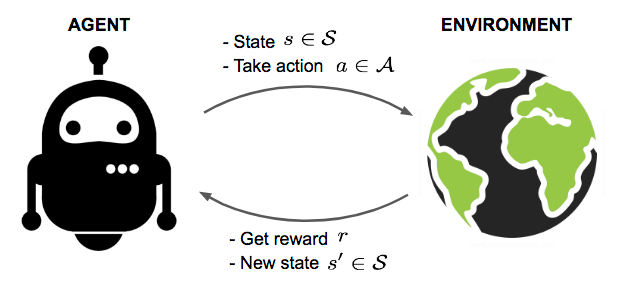
The Markov decision process (MDP) is a mathematical framework for modeling decisions based on a system with a series of states and providing actions to the decision maker based on those states. A partially observable Markov decision process (POMDP) is a generalization of a Markov decision process (MDP). A POMDP models an agent decision process in which it is assumed that the system dynamics are determined by an MDP, but the agent cannot directly observe the underlying state. Instead, there should be a sensor model (the probability distribution of different observations given the underlying state) and the underlying MDP. The policy function in POMDP maps from the history of observations (or belief states) to the actions, in contrast to the policy function in MDP which maps the underlying states to the actions. The POMDP framework is broad enough to describe a range of sequential decision-making processes that occur in the actual world. For each potential belief over the possible world states, an accurate solution to a POMDP produces the best course of action. Over a potentially infinite horizon, the best course of action maximizes predicted gain (or reduces cost) for the actor. The best course of action for an agent to take when interacting with its environment is referred to as the agent’s optimal policy.
The POMPD model how a system can deal with the challenges of limited observation. Because the underlying states of the partially observable Markov decision process are hidden to the agent, the idea of a “belief state” is useful. The belief state offers a solution to the model’s inherent ambiguity. The MPD or POMPD model can be reviewed by a system using what is already known to provide a clearer picture of likely outcomes. This is where the POMPD is helpful in reinforcement learning. Imperfections in the agent’s sensors are one source of ambiguity regarding the real state of the system. The agent cannot know the system’s actual states with a flawed sensor. Here we consider an extension of the (fully observable) MDP setting that also deals with uncertainty resulting from the agent’s imperfect sensors. In general the partial observability stems from two sources: (i) multiple states give the same sensor reading, in case the agent can only sense a limited part of the environment, and (ii) its sensor readings are noisy: observing the same state can result in different sensor readings. The partial observability can lead to “perceptual aliasing”: different parts of the environment appear similar to the agent’s sensor system, but require different actions. The POMDP captures the partial observability in a probabilistic observation model, which relates possible observations to states.
In summary POMDP combines a hidden Markov model that probabilistically links unobservable system states to observations with a normal Markov Decision Process to explain system dynamics. To maximise the projected future rewards that depend on the sequence of system state and the agent’s activities in the future, the agent can take actions that have an impact on the system (i.e., may cause the system state to change). The objective is to identify the best policy to use to direct the agent’s behaviour. In contrast to MDPs, the agent in POMDPs makes observations that depend on the state rather than being able to directly view the entire system state. The agent creates a belief about the state of the system based on these observations. A probability distribution across all potential states is used to express this belief, which is referred to as a belief state. A policy outlining the appropriate course of action for each belief state serves as the POMDP’s solution. Remember that POMDPs are far more challenging to solve than MDPs due to the fact that belief states are continuous, resulting in an endless state set. The POMDP framework is general enough to model a variety of real-world sequential decision-making problems. Applications include robot navigation problems, machine maintenance, and planning under uncertainty in general. POMDPs continue to have many uses, but their understanding is still lacking. This is probably due to the difficulty of the mathematics, the difficulty of using POMDP solvers created by the AI community, and the dearth of necessary resources. This post aims to offer an introduction to POMDPs and instructions on how to define a POMDP in R.
Package Functionality
Solving a POMDP problem with the pomdp package consists of two steps:
- Define a POMDP problem using the function POMDP()
- Solve the problem using solve_POMDP()
Defining a POMDP Problem
The POMDP() function has the following arguments, each corresponds to one of the elements of a POMDP.
str(args(POMDP))
-
States defines the set of states S
-
Actions defines the set of actions A
-
Observations defines the set of observations Ω
-
Transition_prob defines the conditional transition probabilities T(s′∣s,a)
-
Observation_prob specifies the conditional observation probabilities O(o∣s′,a)
-
Reward specifies the reward function R
-
Discount is the discount factor γ in range [0,1]
-
Horizon is the problem horizon as the number of periods to consider.
-
Terminal_values is a vector of state utilities at the end of the horizon.
-
Start is the initial probability distribution over the system states S
-
Max indicates whether the problem is a maximization or a minimization
-
Name used to give the POMDP problem a name.
Solving a POMDP
POMDP problems are solved with the function solve_POMDP(). The list of available parameters can be obtained using the function solve_POMDP_parameter(). Details on the other arguments can be found in the manual page for solve_POMDP().
str(args(solve_POMDP))
-
The horizon argument specifies the finite time horizon (i.e, the number of time steps) considered in solving the problem. If the horizon is unspecified (i.e., NULL), then the algorithm continues running iterations till it converges to the infinite horizon solution.
-
The method argument specifies what algorithm the solver should use. Available methods including “grid”, “enum”, “twopass”, “witness”, and “incprune”. Further solver parameters can be specified as a list in parameters.
Example
Below is the r code with explanation for simulations run in the healthy mood updating network from Modelling mood updating: a proof of principle study.
The following is from the supplementary materials:
- S is a set of hidden states. In this paper the states are “stressful” and “non-stressful”.
- A is a set of possible actions the agent might take. In this paper these are “amplify stress signals”, “attenuate stress signals”, “amplify pleasure signals”, “attenuate pleasure signals” and “wait”.
- T is a transition matrix of prior probabilities in moving between states under a particular action. This varied by mood state (shown in supplemental material). Specific values were chosen in arbitrary way to highlight the principles of mood updating in each mood state.
- R specifies reward, which is a function of action and new state. In our model reward was specified by the surprisal (negative log probability) of each outcome given T. The result is that the agent, in each mood state, must infer the best policy to allow it to minimise surprisal of observations under prior beliefs about the consequences of action.
- Z is a set of possible observations. In this case: “stress signals” or “pleasure signals”.
- O is a probability matrix specifying prior beliefs about the probability of a particular observation given a specific action and resulting hidden state. Again, this changes with each modelled mood state.
- γ is a discount factor between 0 and 1 which determines whether the agent will behave in a short-sighted (maximise immediate expected rewards) or long-sighted (maximise long term expected rewards) way. Recent evidence suggests this have an important role in pathological mood states though, to maximise simplicity, it is set at 0.5 for each of the models in this paper.
Transition probability matrix
In the code a represents the transition probability matrix. The values chosen are arbitrary but designed to reflect the healthy agent’s certainty that action will preserve current belief states. So, for example, if the agent amplifies stress signals then there is a 90% chance the event will be stressful. Intuitviely, waiting will necessarily preserve the current hidden states as they are.
library(pomdp)
a = list("Wait"="identity",
"amplify-stress-signals"= matrix(c(0.9, 0.1, 0.6, 0.4), nrow=2, byrow=TRUE),
"attenuate-stress-signals"= matrix(c(0.4, 0.6, 0.25, 0.75), nrow=2, byrow=TRUE),
"amplify-pleasure-signals"= matrix(c(0.25, 0.75, 0.1, 0.9), nrow=2, byrow=TRUE),
"attenuate-pleasure-signals"= matrix(c(0.75, 0.25, 0.6, 0.4), nrow=2, byrow=TRUE))
|
|
|
|
|
Observation probability matrix
In the code b represents the observation probability matrix. Again this reflects a very certain prior belief in the likely consequences of action matching observations to corresponding hidden states.
b = rbind(
O_("amplify-stress-signals", "Stressful", "Stress-Signals", 0.9),
O_("amplify-stress-signals", "Not-Stressful", "Stress-Signals", 0.3),
O_("amplify-stress-signals", "Stressful", "Pleasure-Signals", 0.1),
O_("amplify-stress-signals", "Not-Stressful", "Pleasure-Signals", 0.7),
O_("attenuate-stress-signals", "Stressful", "Stress-Signals", 0.6),
O_("attenuate-stress-signals", "Not-Stressful", "Stress-Signals", 0.1),
O_("attenuate-stress-signals", "Stressful", "Pleasure-Signals", 0.4),
O_("attenuate-stress-signals", "Not-Stressful", "Pleasure-Signals", 0.9),
O_("amplify-pleasure-signals", "Stressful", "Stress-Signals", 0.6),
O_("amplify-pleasure-signals", "Not-Stressful", "Stress-Signals", 0.1),
O_("amplify-pleasure-signals", "Stressful", "Pleasure-Signals", 0.4),
O_("amplify-pleasure-signals", "Not-Stressful", "Pleasure-Signals", 0.9),
O_("attenuate-pleasure-signals", "Stressful", "Stress-Signals", 0.9),
O_("attenuate-pleasure-signals", "Not-Stressful", "Stress-Signals", 0.4),
O_("attenuate-pleasure-signals", "Stressful", "Pleasure-Signals", 0.1),
O_("attenuate-pleasure-signals", "Not-Stressful", "Pleasure-Signals", 0.6),
O_("Wait", "Stressful", "Stress-Signals", 0.7),
O_("Wait", "Not-Stressful", "Stress-Signals", 0.3),
O_("Wait", "Stressful", "Pleasure-Signals", 0.3),
O_("Wait", "Not-Stressful", "Pleasure-Signals", 0.7))
| action | end.state | observation | probability |
|---|---|---|---|
| amplify-stress-signals | Stressful | Stress-Signals | 0.9 |
| amplify-stress-signals | Not-Stressful | Stress-Signals | 0.3 |
| amplify-stress-signals | Stressful | Pleasure-Signals | 0.1 |
| amplify-stress-signals | Not-Stressful | Pleasure-Signals | 0.7 |
| attenuate-stress-signals | Stressful | Stress-Signals | 0.6 |
| attenuate-stress-signals | Not-Stressful | Stress-Signals | 0.1 |
| attenuate-stress-signals | Stressful | Pleasure-Signals | 0.4 |
| attenuate-stress-signals | Not-Stressful | Pleasure-Signals | 0.9 |
| amplify-pleasure-signals | Stressful | Stress-Signals | 0.6 |
| amplify-pleasure-signals | Not-Stressful | Stress-Signals | 0.1 |
| amplify-pleasure-signals | Stressful | Pleasure-Signals | 0.4 |
| amplify-pleasure-signals | Not-Stressful | Pleasure-Signals | 0.9 |
| attenuate-pleasure-signals | Stressful | Stress-Signals | 0.9 |
| attenuate-pleasure-signals | Not-Stressful | Stress-Signals | 0.4 |
| attenuate-pleasure-signals | Stressful | Pleasure-Signals | 0.1 |
| attenuate-pleasure-signals | Not-Stressful | Pleasure-Signals | 0.6 |
| Wait | Stressful | Stress-Signals | 0.7 |
| Wait | Not-Stressful | Stress-Signals | 0.3 |
| Wait | Stressful | Pleasure-Signals | 0.3 |
| Wait | Not-Stressful | Pleasure-Signals | 0.7 |
Reward matrix
In the code c is the reward matrix. Note that the rewards are framed in terms of the surprisal associated with an end state given a particular action. Thus if the agent amplifies stress signals and the event is non-stressful there is a relative penalty.
c = rbind(
R_("amplify-stress-signals", "Not-Stressful", "*", "*", -1.39),
R_("amplify-stress-signals", "Stressful", "*", "*", -0.29),
R_("attenuate-stress-signals", "Not-Stressful", "*", "*", -0.39),
R_("attenuate-stress-signals", "Stressful", "*", "*", -1.12),
R_("amplify-pleasure-signals", "Not-Stressful", "*", "*", -0.19),
R_("amplify-pleasure-signals", "Stressful", "*", "*", -1.74),
R_("attenuate-pleasure-signals", "Not-Stressful", "*", "*", -1.12),
R_("attenuate-pleasure-signals", "Stressful", "*", "*", -0.39),
R_("Wait", "*", "*", "*", -1))
| action | start.state | end.state | observation | value |
|---|---|---|---|---|
| amplify-stress-signals | Not-Stressful | * | * | -1.39 |
| amplify-stress-signals | Stressful | * | * | -0.29 |
| attenuate-stress-signals | Not-Stressful | * | * | -0.39 |
| attenuate-stress-signals | Stressful | * | * | -1.12 |
| amplify-pleasure-signals | Not-Stressful | * | * | -0.19 |
| amplify-pleasure-signals | Stressful | * | * | -1.74 |
| attenuate-pleasure-signals | Not-Stressful | * | * | -1.12 |
| attenuate-pleasure-signals | Stressful | * | * | -0.39 |
| Wait | * | * | * | -1.00 |
Model
Matrices above are used to compile the model.
HealthyMood <- POMDP(
name = "Healthy Mood",
discount = 0.5,
states = c("Stressful" , "Not-Stressful"),
actions = c("Wait", "amplify-stress-signals", "attenuate-stress-signals", "amplify-pleasure-signals", "attenuate-pleasure-signals"),
observations = c("Stress-Signals", "Pleasure-Signals"),
start = c(0.5, 0.5),
transition_prob = a, observation_prob = b, reward = c)
POMDP, list - Healthy Mood
Discount factor: 0.5
Horizon: Inf epochs
List components: ‘name’, ‘discount’, ‘horizon’, ‘states’, ‘actions’, ‘observations’, ‘transition_prob’, ‘observation_prob’, ‘reward’, ‘start’, ‘terminal_values’
Solution
Then we use the solve_POMDP function to find the optimal solution.
sol <- solve_POMDP(HealthyMood)
sol
POMDP, list - Healthy Mood
Discount factor: 0.5
Horizon: Inf epochs
Solved. Solution converged: TRUE
Total expected reward (for start probabilities): -1.188912
List components: ‘name’, ‘discount’, ‘horizon’, ‘states’, ‘actions’, ‘observations’, ‘transition_prob’, ‘observation_prob’, ‘reward’, ‘start’, ‘solution’, ‘solver_output’
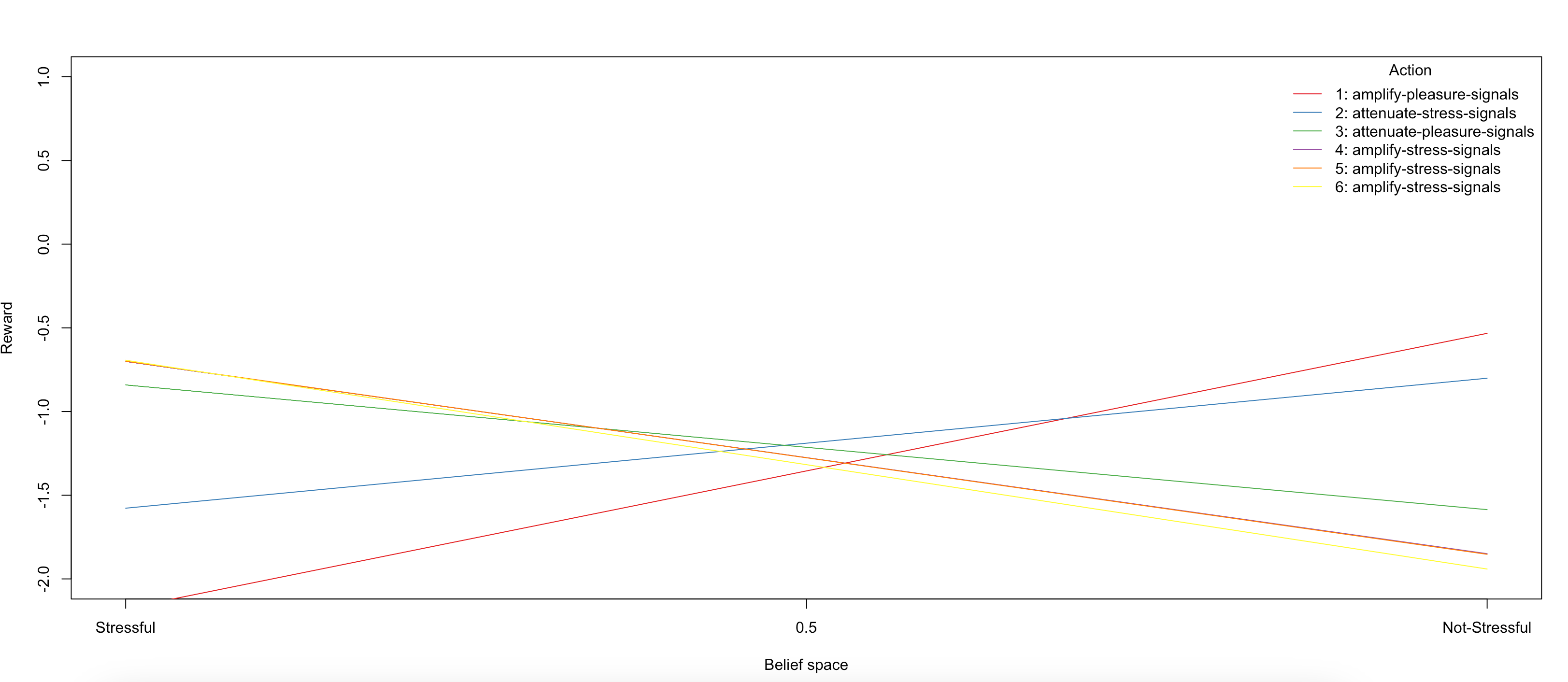
Visualization
Here we will visualize the policy graph provided in the solution by the solve_POMDP() function either with plot_policy_graph
plot_policy_graph(sol)
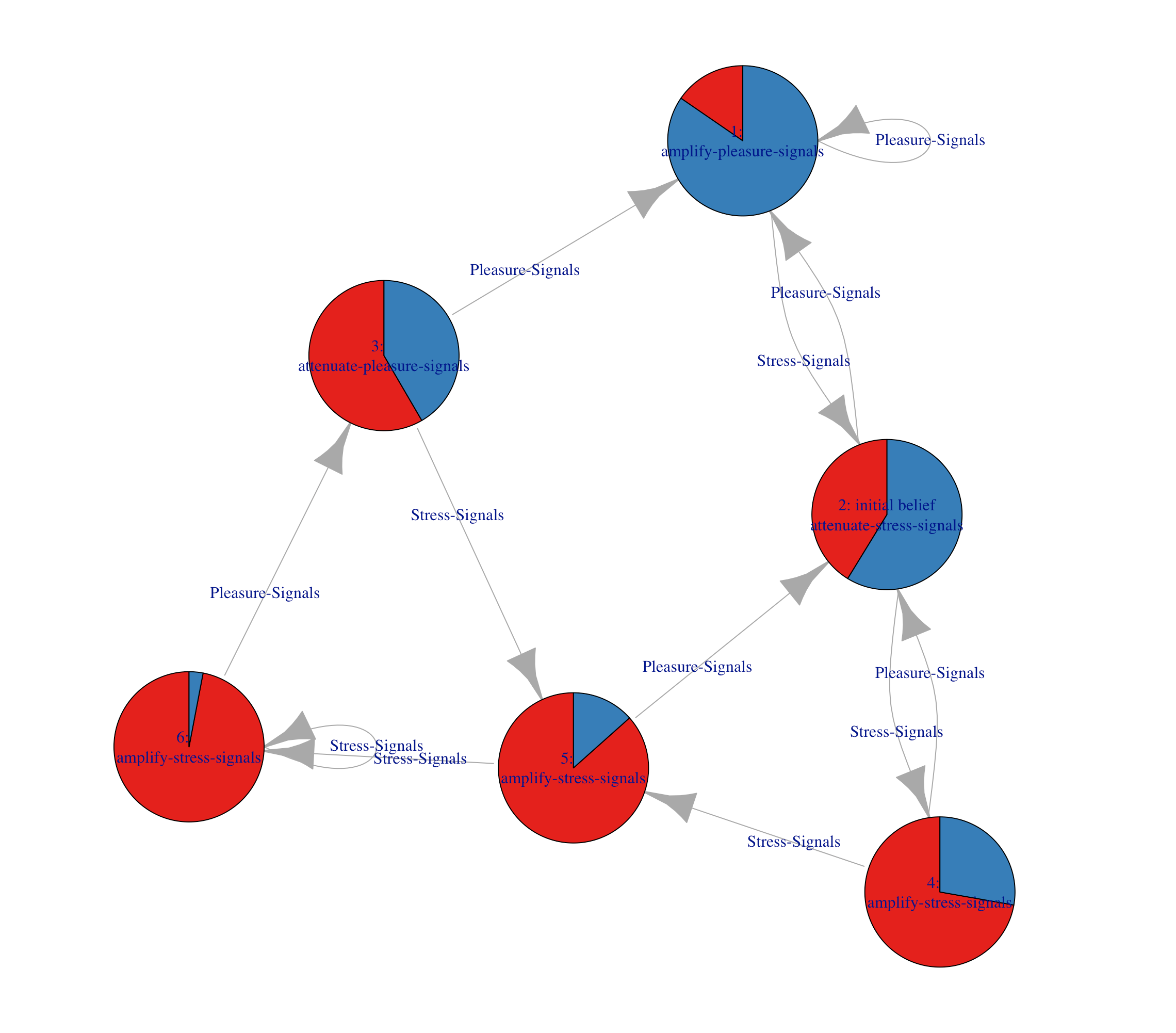
or with plot_policy_graph
plot_value_function(sol, ylim = c(-2,1))
References
-
Clark JE, Watson S. Modelling mood updating: a proof of principle study. Br J Psychiatry. 2023 Mar;222(3):125-134. doi: 10.1192/bjp.2022.175. PMID: 36511113; PMCID: PMC9929713.
- Kurniawati, Hanna, David Hsu, and Wee Sun Lee. 2008. “SARSOP: Efficient Point-Based Pomdp Planning by Approximating Optimally Reachable Belief Spaces.” In In Proc. Robotics: Science and Systems.
- Littman, Michael L., Anthony R. Cassandra, and Leslie Pack Kaelbling. 1995. “Learning Policies for Partially Observable Environments: Scaling up.” In Proceedings of the Twelfth International Conference on International Conference on Machine Learning, 362–70. ICML’95. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc.
- Pineau, Joelle, Geoff Gordon, and Sebastian Thrun. 2003. “Point-Based Value Iteration: An Anytime Algorithm for Pomdps.” In Proceedings of the 18th International Joint Conference on Artificial Intelligence, 1025–30. IJCAI’03. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc.