Quantile regression and its potential for health services
Health services and the necessity of adapted methodology
Multivariate regression techniques are frequently used in health services research publications to assess the association between clinical characteristics, sociodemographic factors, and policy changes (which are typically considered as explanatory variables) and health service utilisation and outcomes. After adjusting for additional explanatory variables, common regression methods evaluate differences in outcome variables between populations at the mean (i.e., ordinary least squares regression), or a population average effect. These are frequently carried out on the presumption that the regression coefficients are constant across the population, meaning that the associations between the important outcomes and the explanatory variables hold true regardless of the values of the variables. However, rather than merely looking at group differences at the mean, researchers, decision-makers, and physicians could be more interested in group differences over the distribution of a given dependent variable.
Another major policy topic that can be evaluated using a method that gauges disparities across the distribution is health care expenditures. When compared to people at the bottom or in the centre of the distribution of health care utilisation, the relationship between health care and health outcomes may be quite different for those who use health care the most frequently. In terms of health status, the average user of healthcare differs greatly from the heavy user, but what about other variables like race/ethnicity, gender, occupation, insurance status, and other variables. In a way that is not conceivable with commonly employed regression techniques, quantile regression enables investigation of these other variations that exist among heavy health care users.
In the US, differences in the distribution of health care spending between Blacks and Whites and between Hispanics and Whites are present at the top quantiles of spending. Even in the top income and educational categories, the same pattern of differences is still noticeable. The assessment of racial and ethnic differences in health care and mental health spending across various quantiles of spending has been done using quantile regression approaches.
OLS vs Quantile regression
Ordinary least squares (OLS) regression and related methods, which typically assume that associations between independent and dependent variables are the same at all levels. Quantile regression is not a regression estimated on a quantile, or subsample of data as the name may suggest. Quantile methods allow the analyst to relax the common regression slope assumption. The objective of OLS regression is to reduce the gaps between the values predicted by the regression line and the values actually observed. In contrast, quantile regression attempts to minimise the weighted distances by differently weighing the distances between the values predicted by the regression line and the observed values. The regression technique known as quantile regression is used to estimate these conditional quantile functions. Quantile regression estimates the conditional quantile function as a linear combination of the predictors, just like linear regression does for the conditional mean function.
Quantile regression is a statistical method that is highly effective and resilient to outliers. Median regression (i.e. 50th quantile regression) is sometimes preferred to linear regression because it is “robust to outliers”. Quantile regression allows you to calculate any desired percentage or quantile for a particular value in the features variables. For instance, if you want to determine the 30th quantile for health expoenses, this means that there is a 30% probability that the actual health expoenses will be below the prediction, while there is a 70% chance that the price will be above it.
Moving forward
The health services literature offers numerous opportunities to use quantile regression. With the advancement of computing power, the time and effort required to estimate quantile regression has significantly reduced. This is evidenced by our study on over 10,000 subjects, which produced results in under a minute. As a result, it has become more feasible to examine interaction terms with observed covariates to determine if slopes are the same or different. With the availability of user-friendly quantile regression commands in widely-used statistical packages, and the reduced time barrier, these methods are expected to become increasingly popular in research projects.
The primary benefit of using quantile regression is that it allows for the examination of relationships between variables beyond the average of the data. This makes it particularly useful in situations where outcomes are not normally distributed and have nonlinear relationships with predictor variables. Common regression methods in health services and outcomes research provide information that is helpful in understanding the typical patient. However, patients with multiple comorbidities, who represent the majority of healthcare expenditures and present the greatest challenge in providing high-quality medical care, are more complex. Quantile regression allows the researcher to avoid assuming that variables operate the same way at the upper tails of the distribution as at the mean, and to identify the key determinants of healthcare costs and quality of care for different patient subgroups.
Quantile regression has additional methodological advantages over other data segmentation methods. For instance, one could argue for running separate regressions that stratify the population based on the unconditional distribution of the dependent variable. In the example of the disparities analysis mentioned earlier, separate regression models could be used to estimate mean expenditures for sub-samples of the population with low, moderate, and high spending. However, segmenting the population in this way can result in smaller sample sizes for each regression and may introduce sample selection issues. In contrast, the quantile regression method assigns weights to different portions of the sample to generate coefficient estimates, which increases the power to detect differences in the upper and lower tails. This approach is superior to truncated regression, which involves segmenting the population based on conditional distributions of the dependent variable.
Code
Here we present a code snippet for the use of quenstile regression in R using the Pima Indians Diabetes Data to predict the glucose levels based on triceps and mass variables.
library(pdp)
data(pima)
med_fit <- rq(glucose ~ triceps + mass, data = pima, tau = 0.5)
q90_fit <- rq(glucose ~ triceps + mass, data = pima, tau = 0.9)
summary(med_fit)
##
## Call: rq(formula = glucose ~ triceps + mass, tau = 0.5, data = pima)
##
## tau: [1] 0.5
##
## Coefficients:
## coefficients lower bd upper bd
## (Intercept) 77.33021 65.47730 87.01627
## triceps 0.35647 -0.05278 0.80306
## mass 0.88180 0.17010 1.41644
summary(q90_fit)
##
## Call: rq(formula = glucose ~ triceps + mass, tau = 0.9, data = pima)
##
## tau: [1] 0.9
##
## Coefficients:
## coefficients lower bd upper bd
## (Intercept) 99.22857 66.07425 141.43019
## triceps 0.31429 -0.25710 0.67261
## mass 1.71429 0.59028 3.03415
new_data <- data.frame(triceps = c(23, 30, 35), mass = c(28, 28, 33))
predict(med_fit, new_data, interval = "confidence")
## fit lower higher
## 1 110.2195 107.1786 113.2604
## 2 112.7148 108.6857 116.7439
## 3 118.9062 114.5386 123.2738
predict(q90_fit, new_data, interval = "confidence")
## fit lower higher
## 1 154.4571 146.3103 162.6040
## 2 156.6571 147.8560 165.4583
## 3 166.8000 159.3241 174.2759
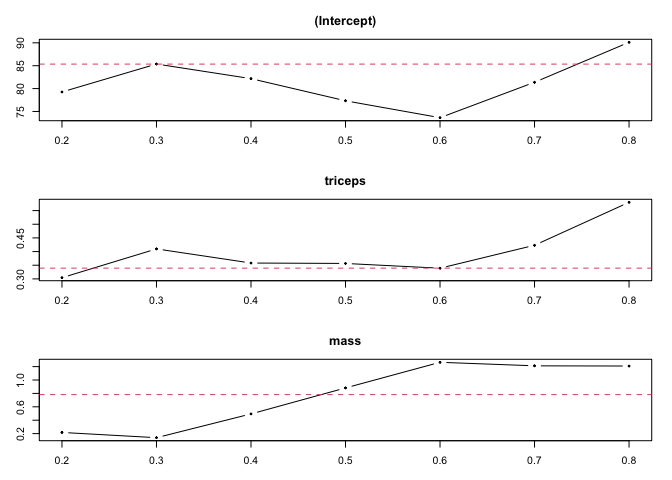
QR=rq(glucose ~ triceps + mass, data = pima, tau=seq(0.2, 0.8, by=0.1))
plot(sumQR)
Reference
-
Zhang, W., Dolan, J. G., & Qian, F. (2014). Thinking beyond the mean: a practical guide for using quantile regression methods for health services research. Shanghai archives of psychiatry, 26(2), 69-76. doi: 10.3969/shpsy.2014.2.69
-
Koenker, R., & Hallock, K. F. (2001). Quantile regression. Journal of Economic perspectives, 15(4), 143-156. doi: 10.1257/jep.15.4.143
-
Cortes, C., & Mohri, M. (2014). Domain adaptation and sample bias correction theory and algorithm for practitioners. arXiv preprint arXiv:1412.4863.
-
Koenker, R. (2005). Quantile regression. Cambridge University Press. doi: 10.1017/cbo9780511754098
-
Yu, B., & Zhang, X. (2005). A study on the relationship between the BMI of children and their parents. Journal of Zhejiang University. Science. B, 6(10), 948-952. doi: 10.1631/jzus.2005.b0948